BYOM, byom_snail_fit.m, DEBkiss with Lymnaea
- Author: Tjalling Jager
- Date: April 2017
- Web support: http://www.debtox.info/byom.html
- Back to index walkthrough_debkiss_paper.html
BYOM is a General framework for simulating model systems in terms of ordinary differential equations (ODEs). The model itself needs to be specified in derivatives.m, and call_deri.m may need to be modified to the particular problem as well. The files in the engine directory are needed for fitting and plotting. Results are shown on screen but also saved to a log file (results.out).
The model: DEBkiss following Jager et al (2013), http://dx.doi.org/10.1016/j.jtbi.2013.03.011.
This script: The case study in the original DEBkiss paper for the pond snail Lymnaea stagnalis at three food levels. The data set was also used in Zimmer et al (2012), http://dx.doi.org/10.1007/s10646-012-0973-5.
Contents
Initial things
Make sure that this script is in a directory somewhere below the BYOM folder.
clear, clear global % clear the workspace and globals global DATA W X0mat % make the data set and initial states global variables global glo % allow for global parameters in structure glo global pri zvd % global structures for optional priors and zero-variate data diary off % turn of the diary function (if it is accidentaly on) % set(0,'DefaultFigureWindowStyle','docked'); % collect all figure into one window with tab controls set(0,'DefaultFigureWindowStyle','normal'); % separate figure windows pathdefine % set path to the BYOM/engine directory glo.basenm = mfilename; % remember the filename for THIS file for the plots glo.saveplt = 0; % save all plots as (1) Matlab figures, (2) JPEG file or (3) PDF (see all_options.txt)
The data set
Data are entered in matrix form, time in rows, scenarios (exposure concentrations) in columns. First column are the exposure times, first row are the concentrations or scenario numbers. The number in the top left of the matrix indicates how to calculate the likelihood:
- -1 for multinomial likelihood (for survival data)
- 0 for log-transform the data, then normal likelihood
- 0.5 for square-root transform the data, then normal likelihood
- 1 for no transformation of the data, then normal likelihood
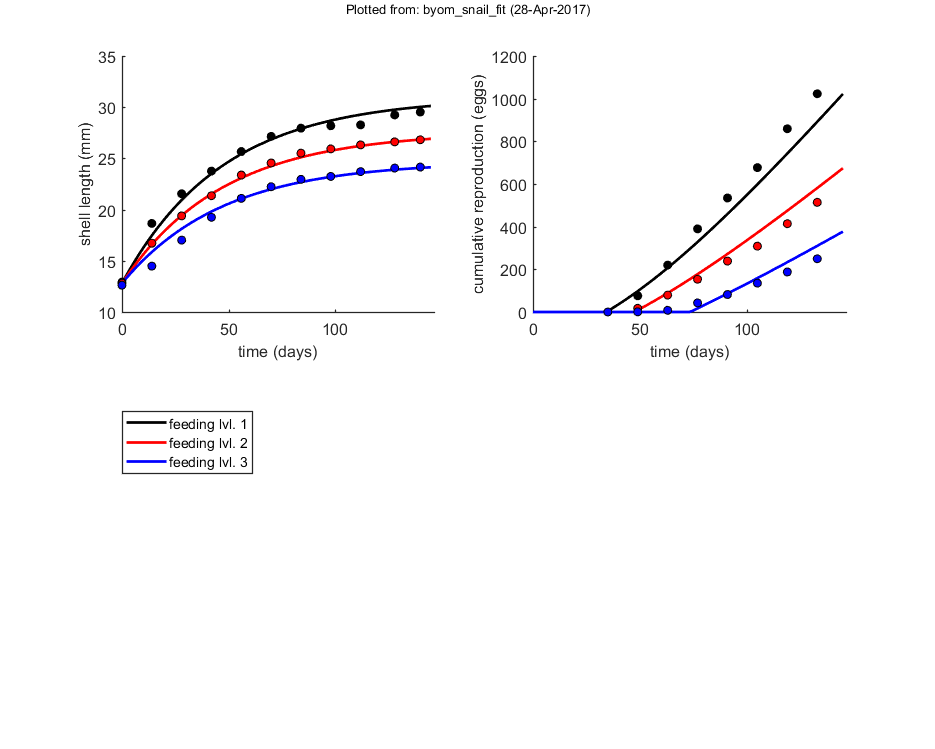
% Shell length in mm over time in three feeding regimes DATA{1} = [0.5 1 2 3 0 12.918 12.799 12.618 14 18.65 16.717 14.479 28 21.549 19.385 17.019 42 23.759 21.357 19.247 56 25.669 23.372 21.095 70 27.146 24.552 22.234 84 27.953 25.514 22.95 98 28.189 25.928 23.238 112 28.27 26.317 23.709 128 29.242 26.614 24.057 140 29.53 26.819 24.153]; % weight factors (number of replicates per observation) W{1} = [30 30 30 30 30 29 29 30 29 28 29 28 28 29 28 26 29 28 26 28 28 26 28 28 25 28 26 23 28 26 21 28 26]; % Cumulative reproduction over time in three feeding regimes; reduced data % to match the frequency of the size measurements (see DEBkiss paper) DATA{2}= [0.5 1 2 3 35 0 0 0 49 76 17.3 0.8 63 219.8 79.3 7.9 77 389.7 153.4 42.6 91 534.6 238.6 82 105 676.8 308.6 135.4 119 858.9 413.9 187.7 133 1023.1 514.1 249.6]; % weight factors (number of replicates per observation) W{2} = [28 29 28 28 29 27 28 29 27 26 29 27 26 28 27 26 28 27 24 28 26 23 28 26]; DATA{3}=0; % no data for the egg buffer (not used in this script) % if weight factors are not specified, ones are assumed in start_calc.m % Notes: In this example, the time vectors are not the same for both data % sets. This is no problem for the analysis.
Initial values for the state variables
Initial states, scenarios in columns, states in rows. First row are the 'names' of all scenarios.
X0mat = [ 1 2 3 % the scenarios (here feeding level) 12.8 12.8 12.8 % initial shell length in mm 0 0 0 % initial cumul repro 0 0 0 ]; % initial weight of buffer in egg
Initial values for the model parameters
Model parameters are part of a 'structure' for easy reference.
% global parameters as part of the structure glo glo.delM = 0.401; % shape corrector (used in call_deri.m) glo.dV = 0.1; % dry weight density (used in call_deri.m) glo.len = 2; % switch to fit physical length (0=off, 1=on, 2=on and no shrinking) (used in call_deri.m) glo.Tlag = 0; % delay for start development (only used for embryo) glo.mat = 0; % include maturity maint. (0=off, 1=include) % Note: if glo.len > 0 than the initial state for size in X0mat is length % too (see call_deri.m) % syntax: par.name = [startvalue fit(0/1) minval maxval optional:log/normal scale (0/1)]; par.sJAm = [0.111 1 0 1e6]; % specific assimilation rate par.sJM = [0.00795 1 0 1e6]; % specific maintenance costs par.WB0 = [0.15 0 0 1e6]; % initial dry weight of egg par.WVp = [70.3 1 0 1e6]; % body mass at puberty par.yAV = [0.8 0 0 1]; % yield of assimilates on volume (starvation) par.yBA = [0.95 0 0 1]; % yield of egg buffer on assimilates par.yVA = [0.8 0 0 1]; % yield of structure on assimilates (growth) par.kap = [0.893 1 0 1]; % allocation fraction to soma par.fB = [1 0 0 2]; % scaled food level, embryo (not used here) par.f1 = [1 0 0 2]; % scaled food level, ad libitum par.f2 = [0.891 1 0 2]; % scaled food level, regime 2 par.f3 = [0.797 1 0 2]; % scaled food level, regime 3 par.WVf = [0 0 0 1e6]; % half-saturation body weight % % Adding the male function % par.sJAm = [0.119 1 0 1e6]; % specific assimilation rate % par.yBA = [0.55 0 0 1]; % yield of egg buffer on assimilates (lowered!) % par.kap = [0.828 1 0 1]; % allocation fraction to soma % % Adding maturity maintenance yields a different fit % glo.mat = 1; % include maturity maint. (0=off, 1=include) % par.sJAm = [0.12 1 0 1e6]; % specific assimilation rate % par.sJM = [0.0078 1 0 1e6]; % specific maintenance costs % par.WVp = [67 1 0 1e6]; % body mass at puberty % par.kap = [0.776 1 0 1]; % allocation fraction to soma % par.f2 = [0.904 1 0 2]; % scaled food level, regime 2 % par.f3 = [0.831 1 0 2]; % scaled food level, regime 3 % par.yBA = [0.95 0 0 1]; % yield of egg buffer on assimilates % % Adding initial food limitation % glo.mat = 1; % include maturity maint. (0=off, 1=include) % par.sJAm = [0.18 1 0 1e6]; % specific assimilation rate % par.sJM = [0.011 1 0 1e6]; % specific maintenance costs % par.WVp = [60.3 1 0 1e6]; % body mass at puberty % par.kap = [0.77 1 0 1]; % allocation fraction to soma % par.f2 = [0.904 1 0 2]; % scaled food level, regime 2 % par.f3 = [0.831 1 0 2]; % scaled food level, regime 3 % par.yBA = [0.55 0 0 1]; % yield of egg buffer on assimilates % par.WVf = [5 1 0 1e6]; % half-saturation body weight
Time vector and labels for plots
Specify what to plot. If time vector glo.t is not specified, a default is used, based on the data set
glo.t = linspace(0,145,100); % time vector for the model simulation in days % specify the y-axis labels for each state variable glo.ylab{1} = 'shell length (mm)'; glo.ylab{2} = 'cumulative reproduction (eggs)'; glo.ylab{3} = 'egg buffer (mg)'; % specify the x-axis label (same for all states) glo.xlab = 'time (days)'; glo.leglab1 = 'feeding lvl. '; % legend label before the 'scenario' number glo.leglab2 = ''; % legend label after the 'scenario' number prelim_checks % script to perform some preliminary checks and set things up % Note: prelim_checks also fills all the options (opt_...) with defauls, so % modify options after this call, if needed.
Calculations and plotting
Here, the function is called that will do the calculation and the plotting. Options for the plotting can be set using opt_plot (see prelim_checks.m). Options for the optimsation routine can be set using opt_optim. Options for the ODE solver are part of the global glo.
For the demo, the iterations are turned off (opt_optim.it = 0).
glo.eventson = 1; % events function on (1) or off (0) opt_optim.fit = 1; % fit the parameters (1), or don't (0) opt_optim.it = 0; % show iterations of the optimisation (1, default) or not (0) opt_plot.bw = 0; % if set to 1, plots in black and white with different plot symbols opt_plot.annot = 2; % annotations in multiplot for fits: 1) box with parameter estimates 2) single legend opt_plot.statsup = [3]; % vector with states to suppress in plotting fits % optimise and plot (fitted parameters in par_out) par_out = calc_optim(par,opt_optim); % start the optimisation calc_and_plot(par_out,opt_plot); % calculate model lines and plot them
Provisional goodness-of-fit measures for each data set
0.9891 0.9733
=================================================================================
Results of the parameter estimation with BYOM version 4.0
=================================================================================
Filename : byom_snail_fit
Analysis date : 28-Apr-2017 (17:01)
Data entered :
data state 1: 11x3, continuous data, power 0.50 transf.
data state 2: 8x3, continuous data, power 0.50 transf.
data state 3: 0x0, no data.
Search method: Nelder-Mead simplex direct search, 2 rounds.
The optimisation routine has converged to a solution
Total 261 simplex iterations used to optimise.
Minus log-likelihood has reached the value 227.673 (AIC=467.347).
=================================================================================
sJAm 0.1106 (fit: 1, initial: 0.111)
sJM 0.007956 (fit: 1, initial: 0.00795)
WB0 0.15 (fit: 0, initial: 0.15)
WVp 70.33 (fit: 1, initial: 70.3)
yAV 0.8 (fit: 0, initial: 0.8)
yBA 0.95 (fit: 0, initial: 0.95)
yVA 0.8 (fit: 0, initial: 0.8)
kap 0.893 (fit: 1, initial: 0.893)
fB 1 (fit: 0, initial: 1)
f1 1 (fit: 0, initial: 1)
f2 0.8913 (fit: 1, initial: 0.891)
f3 0.7972 (fit: 1, initial: 0.797)
WVf 0 (fit: 0, initial: 0)
=================================================================================
Time required: 12.2 secs
Plots result from the optimised parameter values.
Profiling the likelihood
By profiling you make robust confidence intervals for one or more of your parameters. Use the name of the parameter as it occurs in your parameter structure par above. You do not need to run the entire script before you can make a profile.
Options for the profiling can be set using opt_prof (see prelim_checks). For this demo, the level of detail of the profiling is set to 'course' and no sub-optimisations are used. However, consider these options when working on your own data (e.g., set opt_prof.subopt=10).
opt_prof.detail = 2; % detailed (1) or a course (2) calculation opt_prof.subopt = 0; % number of sub-optimisations to perform to increase robustness % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % run a profile for selected parameters ... % calc_proflik(par_out,'sJAm',opt_prof); % calculate a profile % calc_proflik(par_out,'sJM',opt_prof); % calculate a profile % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % or run profiles for all fitted parameters. % all_profiles(par_out,opt_prof); % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % Automatically calculate profiles for all parameters, and redo % % optimisation when a better value is found. % opt_prof.subopt = -1; % number of sub-optimisations to perform to increase robustness % % Note: the -1 makes a comparison between 0 and 10 sub-optimisations. % % In this example, sub-optimisations are helpful! % par_out = auto_profiles(par_out,opt_prof,opt_optim); % Experimental!
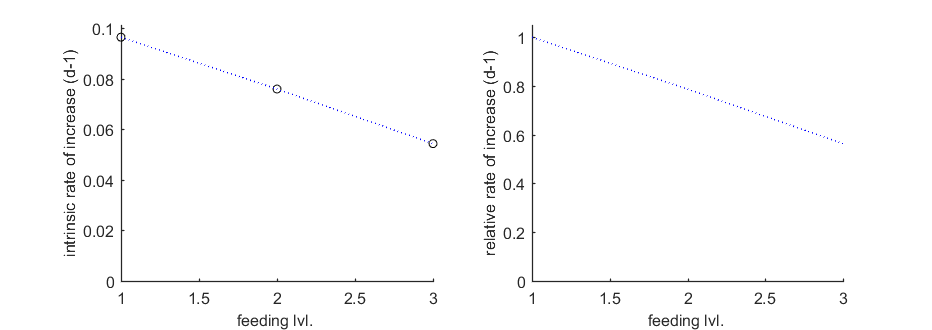
Population growth rate
The function calc_pop allows for a calculation of the intrinsic rate of population increase (Euler-Lotka equation). It calculates the growth rate at three food levels (set in the engine file calc_pop.m). Note that two plots are made: the absolute growth rate and the relative one.
Tpop = linspace(0,300,100); % time vector for the population calculations Cpop = -1; % use only feeding levels as given in X0mat Th = 10; % time from fresh egg to t=0 in time vector (e.g., hatching time) trep = [0]; % vector with reproduction events (first one must be a zero) % here, zero to base calculation on continuous reproduction calc_pop(par_out,X0mat,[-1 2],Tpop,Cpop,Th,trep)
Other files: derivatives
To archive analyses, publishing them with Matlab is convenient. To keep track of what was done, the file derivatives.m can be included in the published result.
%% BYOM function derivatives.m (the model in ODEs) % % Syntax: dX = derivatives(t,X,par,c) % % This function calculates the derivatives for the model system. It is % linked to the script files for the snails in the DEBkiss1 package. As % input, it gets: % % * _t_ is the time point, provided by the ODE solver % * _X_ is a vector with the previous value of the states % * _par_ is the parameter structure % * _c_ is the external concentration (or scenario number) % % Time _t_ and scenario name _c_ are handed over as single numbers by % <call_deri.html call_deri.m> (you do not have to use them in this % function). Output _dX_ (as vector) provides the differentials for each % state at _t_. % % * Author: Tjalling Jager % * Date: April 2017 % * Web support: <http://www.debtox.info/byom.html> % * Back to index <walkthrough_debkiss_paper.html> %% Start function dX = derivatives(t,X,par,c) global glo % allow for global parameters in structure glo %% Unpack states % The state variables enter this function in the vector _X_. Here, we give % them a more handy name. WV = X(1); % state 1 is the structural body mass cR = X(2); % state 2 is the cumulative reproduction (not used here) WB = X(3); % state 3 is the egg buffer of assimilates WV = max(0,WV); % for poor choice of paramaters, WV can become nagtive, which smothers the ODE solver %% Unpack parameters % The parameters enter this function in the structure _par_. The names in % the structure are the same as those defined in the byom script file. % The 1 between parentheses is needed as each parameter has 5 associated % values. Tlag = glo.Tlag; % lag time for start embryo development dV = glo.dV; % dry weight density of structure if c==1 Tlag = 0; % the c=1 scenario for embryos does not include a lag time % for the juvenile/adult runs, this does not hurt as Tlag=0 anyway end sJAm = par.sJAm(1); % specific assimilation rate sJM = par.sJM(1); % specific maintenance costs WB0 = par.WB0(1); % initial weight of egg WVp = par.WVp(1); % body mass at puberty yAV = par.yAV(1); % yield of assimilates on volume (starvation) yBA = par.yBA(1); % yield of egg buffer on assimilates yVA = par.yVA(1); % yield of structure on assimilates (growth) kap = par.kap(1); % allocation fraction to soma f1 = par.f1(1); % scaled food level, ad libitum f2 = par.f2(1); % scaled food level, regime 2 f3 = par.f3(1); % scaled food level, regime 3 fB = par.fB(1); % scaled food level for the embryo (adapted model) WVf = par.WVf(1); % half-saturation size for initial food limitation %% Calculate the derivatives % This is the actual model, specified as a system of ODEs. % Note: some unused fluxes are calculated because they may be needed for % future modules (e.g., respiration and ageing). L = (WV/dV)^(1/3); % volumetric length from dry weight % select what to do with maturity maintenance if glo.mat == 1 sJJ = sJM * (1-kap)/kap; % add specific maturity maintenance with the suggested value else sJJ = 0; % or ignore it end WVb = WB0 *yVA * kap; % predicted body mass at birth if WB > 0 % if we have an embryo (run from byom_snail_embryo.m) if c==2 % for the 'adapted' scenario ... f = fB; % assimilation at limited rate else % for the 'standard' scenario f = 1; % assimilation at maximum rate end else % we have jubeniles/adults (run from byom_snail_fit.m or byom_snail_starv.m) switch c % run through the three feeding regimes to select proper f case 1 f = f1; case 2 f = f2; yAV = 7*0.8; % this is used for the adapted starvation simulation % no problem if it is also on for the fits, as there is no % starvation occurring there anyway! case 3 f = f3; end if WVf > 0 f = f / (1+WVf/WV); % hyperbolic relationship for f with body weight end end % if WV < WVb && WB <= 0 % error('Your animal is initiated or has shrunk to less than the size at birth! Increase the start weight or check the food levels.') % end JA = f * sJAm * L^2; % assimilation JM = sJM * L^3; % somatic maintenance JV = yVA * (kap*JA-JM); % growth if WV < WVp % below size at puberty JR = 0; % no reproduction JJ = sJJ * L^3; % maturity maintenance flux % JH = (1-kap) * JA - JJ; % maturation flux (not used!) else JJ = sJJ * (WVp/dV); % maturity maintenance JR = (1-kap) * JA - JJ; % reproduction flux end % starvation rules may override these fluxes if kap * JA < JM % allocated flux to soma cannot pay maintenance if JA >= JM + JJ % but still enough total assimilates to pay both maintenances JV = 0; % stop growth if WV >= WVp % for adults ... JR = JA - JM - JJ; % repro buffer gets what's left else % JH = JA - JM - JJ; % maturation gets what's left (not used!) end elseif JA >= JM % only enough to pay somatic maintenance JV = 0; % stop growth JR = 0; % stop reproduction % JH = 0; % stop maturation for juveniles (not used) JJ = JA - JM; % maturity maintenance flux gets what's left else % we need to shrink JR = 0; % stop reproduction JJ = 0; % stop paying maturity maintenance % JH = 0; % stop maturation for juveniles (not used) JV = (JA - JM) / yAV; % shrink; pay somatic maintenance from structure end end % we do not work with a repro buffer here, so a negative JR does not make % sense; therefore, minimise to zero JR = max(0,JR); % Calcululate the derivatives dWV = JV; % change in body mass dcR = yBA * JR / WB0; % continuous reproduction flux if WB > 0 % for embryos ... dWB = -JA; % decrease in egg buffer else dWB = 0; % for juveniles/adults, no change end if WV < WVb/4 && dWB == 0 % dont shrink below quarter size at birth dWV = 0; % simply stop shrinking ... end if t < Tlag dX = [0;0;0]; else dX = [dWV;dcR;dWB]; % collect both derivatives in one vector end
Other files: call_deri
To archive analyses, publishing them with Matlab is convenient. To keep track of what was done, the file call_deri.m can be included in the published result.
%% BYOM function call_deri.m (calculates the model output) % % Syntax: [Xout TE] = call_deri(t,par,X0v) % % This function calls the ODE solver to solve the system of differential % equations specified in <derivatives.html derivatives.m>, or the explicit % function(s) in <simplefun.html simplefun.m>. As input, it gets: % % * _t_ the time vector % * _par_ the parameter structure % * _X0v_ a vector with initial states and one concentration (scenario number) % % The output _Xout_ provides a matrix with time in rows, and states in % columns. This function calls <derivatives.html derivatives.m>. The % optional output _TE_ is the time at which an event takes place (specified % using the events function). The events function is set up to catch % discontinuities. It should be specified according to the problem you are % simulating. If you want to use parameters that are (or influence) initial % states, they have to be included in this function. % % * Author: Tjalling Jager % * Date: April 2017 % * Web support: <http://www.debtox.info/byom.html> % * Back to index <walkthrough_debkiss_paper.html> %% Start function [Xout TE Xout2] = call_deri(t,par,X0v) global glo % allow for global parameters in structure glo global zvd % global structure for zero-variate data % NOTE: this file is modified so that data and output can be as body length % whereas the state variable remains body weight. Also, there is a % calculation to prevent shrinking in physical length (as shells, for % example, do not shrink). %% Initial settings % This part can be modified by the user to decide whether to calculate the % model results using the ODEs in <derivatives.html derivatives.m>, or the % analytical solution in <simplefun.html simplefun.m>. Further, the events % function can be turned on here, initial values can be determined by a % parameter, and zero-variate data can be calculated. useode = glo.useode; % calculate model using ODE solver (1) or analytical solution (0) eventson = glo.eventson; % events function on (1) or off (0) stiff = glo.stiff; % set to 1 to use a stiff solver instead of the standard one % Unpack the vector X0v, which is X0mat for one scenario X0 = X0v(2:end); % these are the intitial states for a scenario % if needed, extract parameters from par that influence initial states in X0 % % start from specified initial size % Lw0 = par.Lw0(1); % initial body length (mm) % X0(2) = glo.dV*((Lw0*glo.delM)^3); % recalculate to dwt, and put this parameter in the correct location of the initial vector % start from the value provided in X0mat if glo.len ~= 0 % only if the switch is set to 1 or 2! % Assume that X0mat includes initial length; if it includes mass, no correction is needed here % The model is set up in masses, so we need to translate the initial length % (in mm body length) to body mass using delM. Assume that size is first state. X0(1) = glo.dV*((X0(1) * glo.delM)^3); % initial length to initial dwt end % % start at hatching, so calculate initial length from egg weight % WB0 = par.WB0(1); % initial dry weight of egg % yVA = par.yVA(1); % yield of structure on assimilates (growth) % kap = par.kap(1); % allocation fraction to soma % WVb = WB0 *yVA * kap; % dry body mass at birth % X0(2) = WVb; % put this estimate in the correct location of the initial vector % % if needed, calculate model values for zero-variate data from parameter set % if ~isempty(zvd) % zvd.ku(3) = par.Piw(1) * par.ke(1); % add model prediction as third value % end %% Calculations % This part calls the ODE solver (or the explicit model in <simplefun.html % simplefun.m>) to calculate the output (the value of the state variables % over time). There is generally no need to modify this part. The solver % ode45 generally works well. For stiff problems, the solver might become % very slow; you can try ode15s instead. c = X0v(1); % the concentration (or scenario number) t = t(:); % force t to be a row vector (needed when useode=0) % specify options for the ODE solver options = odeset; % start with default options if eventson == 1 options = odeset(options, 'Events',@eventsfun); % add an events function end options = odeset(options, 'RelTol',1e-4,'AbsTol',1e-7); % specify tightened tolerances % options = odeset(options,'InitialStep',max(t)/1000,'MaxStep',max(t)/100); % specify smaller stepsize if useode == 1 % use the ODE solver to calculate the solution % call the ODE solver (use ode15s for stiff problems, escpecially for pulses) if isempty(options.Events) % if no events function is specified ... switch stiff case 0 [~,Xout] = ode45(@derivatives,t,X0,options,par,c); case 1 [~,Xout] = ode113(@derivatives,t,X0,options,par,c); case 2 [~,Xout] = ode15s(@derivatives,t,X0,options,par,c); end else % with an events functions ... additional output arguments for events: % TE catches the time of an event, YE the states at the event, and IE the number of the event switch stiff case 0 [~,Xout,TE,YE,IE] = ode45(@derivatives,t,X0,options,par,c); case 1 [~,Xout,TE,YE,IE] = ode113(@derivatives,t,X0,options,par,c); case 2 [~,Xout,TE,YE,IE] = ode15s(@derivatives,t,X0,options,par,c); end end else % alternatively, use an explicit function provided in simplefun! Xout = simplefun(t,X0,par,c); end if isempty(TE) || all(TE == 0) % if there is no event caught TE = +inf; % return infinity end %% Output mapping % _Xout_ contains a row for each state variable. It can be mapped to the % data. If you need to transform the model values to match the data, do it % here. % here, translate from the state body weight to output in length, if needed if glo.len ~= 0 % only if the switch is set to 1 or 2! % Here, I translate the model output in body mass to estimated physical body length W = Xout(:,1); % Assume that dry body weight is the first state Lw = (W/glo.dV).^(1/3)/glo.delM; % estimated physical body length if glo.len == 2 % when animal cannot shrink in length (but does on volume!) maxLw = 0;%zeros(size(Lw)); % remember max size achieved for i = 1:length(Lw) % run through length data maxLw = max([maxLw;Lw(i)]); % new max is max of old max and previous size Lw(i) = maxLw; % replace value in output vector end end Xout(:,1) = Lw; % replace body weight by physical body length end % % To obtain the output of the derivatives at each time point. The values in % % dXout might be used to replace values in Xout, if the data to be fitted % % are the changes (rates) instead of the state variable itself. % % dXout = zeros(size(Xout)); % initialise with zeros % for i = 1:length(t) % run through all time points % dXout(i,:) = derivatives(t(i),Xout(i,:),par,c); % % derivatives for each stage at each time % end % the part below is highly modified for the specific calculations in the % DEBkiss1 package, to reproduce the figures in the DEBkiss publication if X0v(4) > 0 % there is an initial repro buffer, so we started with a fresh egg! Xout(t>TE,1) = NaN; % don't include body length after point of hatching end % next, calculate respiration from the body length data Lw = Xout(:,1); % shell length from the output matrix (state 1) LV = Lw*glo.delM; % translate to volumetric length JA = par.sJAm(1)*(LV.^2); % embryo assimilation rate for f=1 JA = JA * par.fB(1); % calculate with reduced f for the embryo JM = par.sJM(1)*(LV.^3); % flux for maintenance JV = par.yVA(1)*(par.kap(1)*JA-JM); % flux fixed in structural biomass JD = JA - JV; % dissipation is assimilation minus what is fixed in growth Resp = JD * 130; % proportionality is uL O2/mg dissipated assimilates (see paper) Resp(t<glo.Tlag(1),:) = 0; % during the lag phase, assume no respiration Resp(t>TE,:) = NaN; % don't include respiration after hatching Xout2{1}(:,1) = t; % time is on the x-axis of the extra data set Xout2{1}(:,2) = Resp; % repiration on the y-axis %% Events function % Modify this part of the code if _eventson_=1. This subfunction catches % the 'events': in this case, this one catches birth and puberty. % % Note that the eventsfun has the same inputs, in the same sequence, as % <derivatives.html derivatives.m>. function [value,isterminal,direction] = eventsfun(t,X,par,c) WVp = par.WVp(1); % body mass at puberty nevents = 2; % number of events that we try to catch value = zeros(nevents,1); % initialise with zeros value(1) = X(1) - WVp; % thing to follow is body mass (state 1) minus threshold value(2) = X(3); % follow the egg buffer (state 1) to spot hatching isterminal = zeros(nevents,1); % do NOT stop the solver at an event direction = zeros(nevents,1); % catch ALL zero crossing when function is increasing or decreasing