BYOM, byom_gutsred_timevar_diazinon.m, reduced GUTS model
- Author: Tjalling Jager
- Date: September 2018
- Web support: http://www.debtox.info/byom.html
- Back to index walkthrough_guts.html
BYOM is a General framework for simulating model systems.
The model: fitting survival data with the GUTS special cases based on the reduced model (TK and damage dynamics lumped): SD, IT and mixed (or GUTS proper).
This script: dataset from Ashauer et al. (2010), http://dx.doi.org/10.1021/es903478b. Gammarus pulex exposed to pulses of diazinon. One scenario from this data set (two pulses) was used in Jager (2014), http://dx.doi.org/10.1007/s10646-013-1149-7. This script demonstrates two ways to define time-varying exposure scenarios: as a continuous spline or as a series of episodes.
Contents
- Initial things
- The data set
- Initial values for the state variables
- Initial values for the model parameters
- Time vector and labels for plots
- Calculations and plotting
- Profiling the likelihood
- Likelihood region
- Plot results with confidence intervals
- Calculate LPx
- Calculate LCx versus time
- Calculate LPx for a monitoring profile
Initial things
Make sure that this script is in a directory somewhere below the BYOM folder.
clear, clear global % clear the workspace and globals global DATA W X0mat % make the data set and initial states global variables global glo % allow for global parameters in structure glo global pri zvd % global structures for optional priors and zero-variate data diary off % turn of the diary function (if it is accidentaly on) % set(0,'DefaultFigureWindowStyle','docked'); % collect all figure into one window with tab controls set(0,'DefaultFigureWindowStyle','normal'); % separate figure windows pathdefine % set path to the BYOM/engine directory glo.basenm = mfilename; % remember the filename for THIS file for the plots glo.saveplt = 0; % save all plots as (1) Matlab figures, (2) JPEG file or (3) PDF (see all_options.txt)
The data set
Data are entered in matrix form, time in rows, scenarios (exposure concentrations) in columns. First column are the exposure times, first row are the concentrations or scenario numbers. The number in the top left of the matrix indicates how to calculate the likelihood:
- -1 for multinomial likelihood (for survival data)
- 0 for log-transform the data, then normal likelihood
- 0.5 for square-root transform the data, then normal likelihood
- 1 for no transformation of the data, then normal likelihood
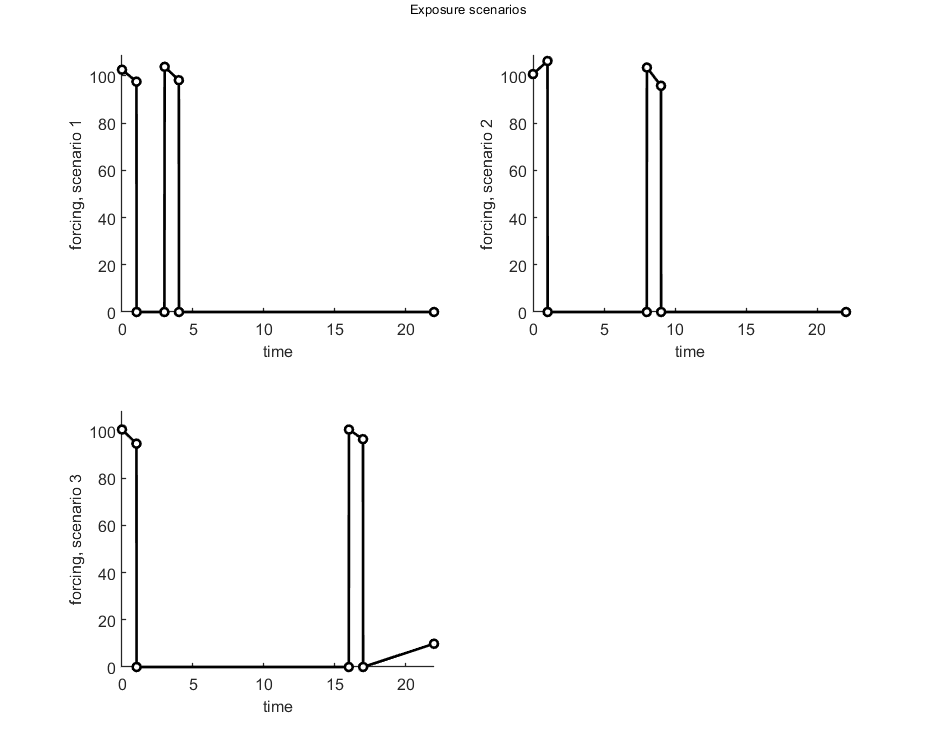
% observed number of survivors, time in days, conc in nM DATA{1} = [-1 0 1 2 3 0 60 70 70 70 1 55 66 65 65 2 53 61 59 59 3 51 55 56 55 4 51 31 54 53 5 51 31 50 51 6 51 29 47 48 7 48 26 46 46 8 48 24 46 46 9 46 22 40 46 10 45 21 23 44 11 44 19 22 41 12 42 17 22 40 13 41 14 21 40 14 41 14 18 40 15 40 13 17 39 16 38 11 17 38 17 38 11 13 36 18 37 10 13 33 19 37 9 13 28 20 37 8 11 24 21 37 8 11 23 22 36 8 11 19]; % In this data set, exposure was time-varying and reported as a series of % concentrations over time. BYOM offers several ways to deal with it, as % show below. % % Define the exposure scenarios as a series of pulses with a new constant % exposure in each time period. This allow use of an analytical solution % for the TK/damage dynamics in simplefun. This is a simplification of the % reported exposure scenario, which has almost, but not quite, constant % pulses in each episode. % Cw1 = [0 1 % scenario 1 % 0 100.12 % 1 0 % 3 101.04 % 4 0]; % Cw2 = [0 2 % scenario 2 % 0 103.55 % 1 0 % 8 99.69 % 9 0]; % Cw3 = [0 3 % scenario 3 % 0 97.61 % 1 0 % 16 98.55 % 17 0]; % % make_scen(2,Cw1,Cw2,Cw3); % create the globals to define the forcing function % We can also use the exposure pattern exactly as reported. There are two % ways to use this in BYOM: create a smooth spline (and use the ODE solver) % or as a linear forcing series (which has an anlytical solution, and is % thus much faster than the previous one). Cw1 = [0 1 0 102.65 1.02 97.59 1.03 0 2.99 0 3.01 103.88 4.01 98.19 4.02 0 22.01 0]; Cw2 = [0 2 0 100.78 1.02 106.32 1.03 0 8 0 8.01 103.56 9 95.82 9.01 0 22.01 0]; Cw3 = [0 3 0 100.6 1.02 94.61 1.03 0 16 0 16.01 100.58 17 96.51 17.01 0 22.01 9.85]; make_scen(4,Cw1,Cw2,Cw3); % prepare as linear-forcing function interpolation (set glo.use_ode = 0) % make_scen(1,Cw1,Cw2,Cw3); % prepare as cubic spline for interpolation (set glo.use_ode = 1) % internal concentrations DATA{2} = 0; % no data for scaled body residues
Initial values for the state variables
Initial states, scenarios in columns, states in rows. First row are the 'names' of all scenarios.
X0mat(1,:) = [0 1 2 3]; % scenarios (pulses) X0mat(2,:) = 1; % initial survival probability X0mat(3,:) = 0; % initial internal concentration
Initial values for the model parameters
Model parameters are part of a 'structure' for easy reference.
% global parameters for GUTS purposes glo.sel = 1; % select death mechanism: 1) SD 2) IT 3) mixed glo.locD = 2; % location of scaled damage in the state variable list glo.locS = 1; % location of survival probability in the state variable list % Best values SD % syntax: par.name = [startvalue fit(0/1) minval maxval optional:log/normal scale (0/1)]; par.kd = [0.083 1 1e-3 10 0]; % dominant rate constant (d-1) par.mw = [4.8 1 0 1e6 1]; % median threshold for survival (nM) par.hb = [0.027 1 0 1e6 1]; % background hazard rate (1/d) par.bw = [0.023 1 0 1e3 0]; % killing rate (nM-1 d-1) (SD and mixed) par.Fs = [2 1 1 100 1]; % fraction spread of NEC distribution (-) (IT and mixed) switch glo.sel % make sure that right parameters are fitted case 1 % SD par.Fs(2) = 0; % never fit the NEC spread! case 2 % IT par.bw(2) = 0; % never fit the killing rate! case 3 % mixed % do nothing: fit all parameters end
Time vector and labels for plots
Specify what to plot. If time vector glo.t is not specified, a default is used, based on the data set
% specify the y-axis labels for each state variable glo.ylab{1} = 'survival probability'; glo.ylab{2} = 'scaled damage (nM)'; % specify the x-axis label (same for all states) glo.xlab = 'time (days)'; glo.leglab1 = 'scenario '; % legend label before the 'scenario' number glo.leglab2 = ''; % legend label after the 'scenario' number prelim_checks % script to perform some preliminary checks and set things up % Note: prelim_checks also fills all the options (opt_...) with defauls, so % modify options after this call, if needed.
Calculations and plotting
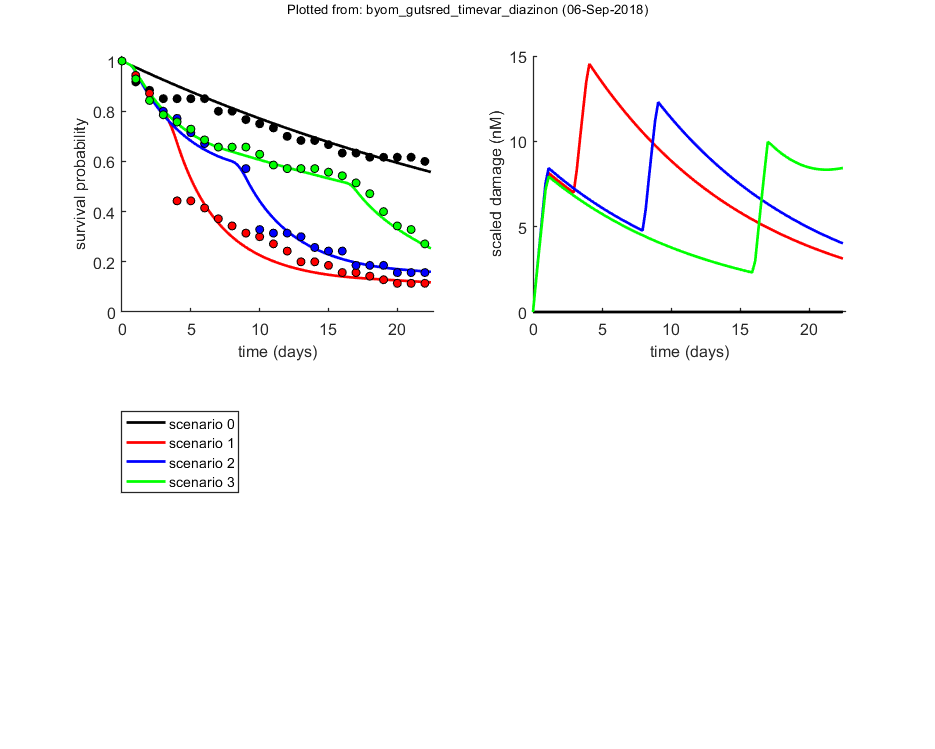
Here, the function is called that will do the calculation and the plotting.
glo.useode = 0; % use analytical solution in simplefun (0) or ODE solver (1) glo.stiff = 1; % use ode113: works best with small step sizes needed for splined scenarios if glo.sel == 1 % for the pure SD model, turn on the events function to catch threshold exceedance glo.eventson = 1; % events function on (1) or off (0) end opt_plot.annot = 2; % annotations in multiplot for fits: 1) box with parameter estimates 2) single legend opt_optim.fit = 1; % fit the parameters (1), or don't (0) opt_optim.it = 0; % show iterations of the optimisation (1, default) or not (0) % optimise and plot (fitted parameters in par_out) par_out = calc_optim(par,opt_optim); % start the optimisation calc_and_plot(par_out,opt_plot); % calculate model lines and plot them % opt_guts.doseresp = 0; % set to zero as a dose-response is meaningless for time-var. exposure % plot_guts(par_out,[],opt_guts); % make GUTS multiplots, but without CIs
Goodness-of-fit measures for each data set (R-square)
0.9763
Warning: R-square is not appropriate for survival data and needs to be
interpreted more qualitatively!
=================================================================================
Results of the parameter estimation with BYOM version 4.2b
=================================================================================
Filename : byom_gutsred_timevar_diazinon
Analysis date : 06-Sep-2018 (13:47)
Data entered :
data state 1: 23x4, survival data.
data state 2: 0x0, no data.
Search method: Nelder-Mead simplex direct search, 2 rounds.
The optimisation routine has converged to a solution
Total 114 simplex iterations used to optimise.
Minus log-likelihood has reached the value 692.624 (AIC=1393.25).
=================================================================================
kd 0.08359 (fit: 1, initial: 0.083)
mw 4.675 (fit: 1, initial: 4.8)
hb 0.02601 (fit: 1, initial: 0.027)
bw 0.02281 (fit: 1, initial: 0.023)
Fs 2 (fit: 0, initial: 2)
=================================================================================
Parameters kd and bw are fitted on log-scale.
=================================================================================
Time required: 0.6 secs
Plots result from the optimised parameter values.
Profiling the likelihood
By profiling you make robust confidence intervals for one or more of your parameters.
opt_prof.detail = 2; % detailed (1) or a coarse (2) calculation opt_prof.subopt = 10; % number of sub-optimisations to perform to increase robustness % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % run a profile for selected parameters ... % calc_proflik(par_out,'kd',opt_prof); % uncomment to calculate a profile % calc_proflik(par_out,'mw',opt_prof); % uncomment to calculate a profile
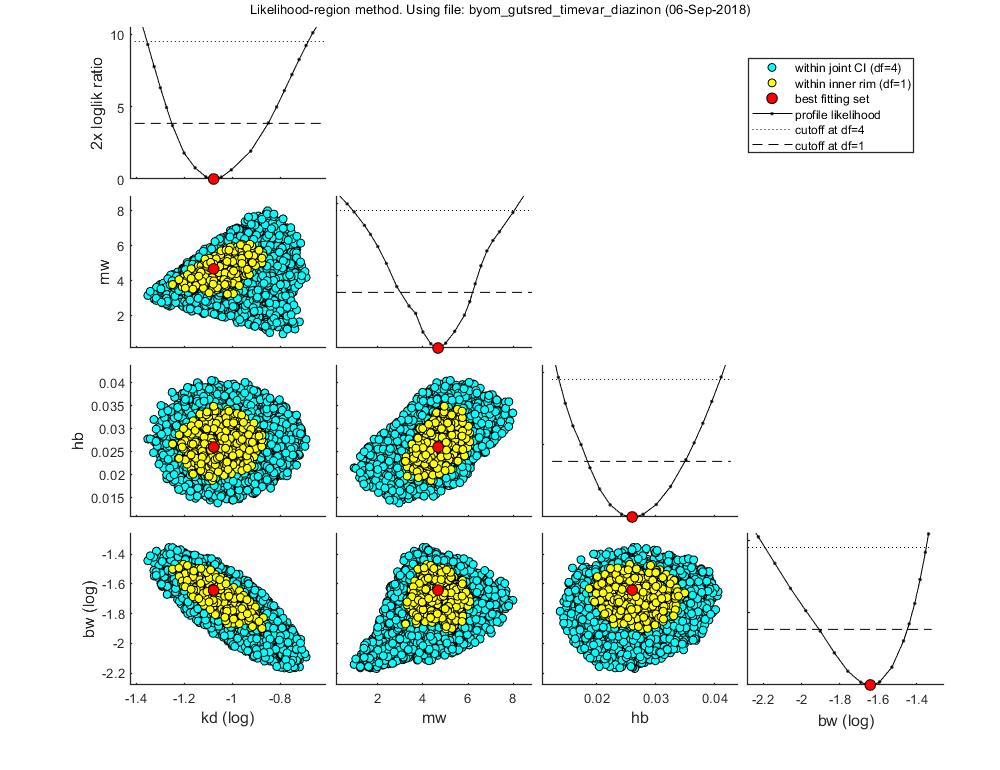
Likelihood region
Make intervals on model predictions by using a sample of parameter sets taken from the joint likelihood-based conf. region.
% UNCOMMENT FOLLOWING LINE(S) TO CALCULATE opt_likreg.subopt = 10; % number of sub-optimisations to perform to increase robustness opt_likreg.detail = 2; % detailed (1) or a coarse (2) calculation opt_likreg.burst = 2000; % number of random samples from parameter space taken every iteration calc_likregion(par_out,500,opt_likreg); % second argument number of samples (-1 to re-use saved sample from previous runs)
Calculating profiles and sample from confidence region ... please be patient. Confidence interval from the profile (single parameter, 95% confidence) ================================================================================= kd interval: 0.05594 - 0.1411 mw interval: 3.01 - 6.203 hb interval: 0.01845 - 0.03496 bw interval: 0.01232 - 0.03564 Edges of the joint 95% confidence region (using df=p) ================================================================================= kd interval: 0.04409 - 0.207 mw interval: 0.9108 - 8.043 hb interval: 0.01361 - 0.04091 bw interval: 0.006432 - 0.04467 Starting with obtaining a sample from the joint confidence region. Bursts of 2000 samples, until at least 500 samples are accepted in inner rim. Currently accepted (inner rim): 0, 11, 22, 30, 37, 47, 51, 57, 66, 78, 91, 97, 108, 118, 127, 136, 146, 157, 166, 177, 187, 194, 210, 217, 229, 238, 246, 255, 264, 275, 284, 293, 302, 311, 318, 331, 341, 346, 351, 362, 370, 378, 387, 398, 406, 414, 423, 435, 445, 453, 462, 473, 483, 494, Size of total sample (profile points have been added): 108085 of which accepted in the conf. region: 4458, and in inner rim: 551 Time required: 9 mins, 6.2 secs
Plot results with confidence intervals
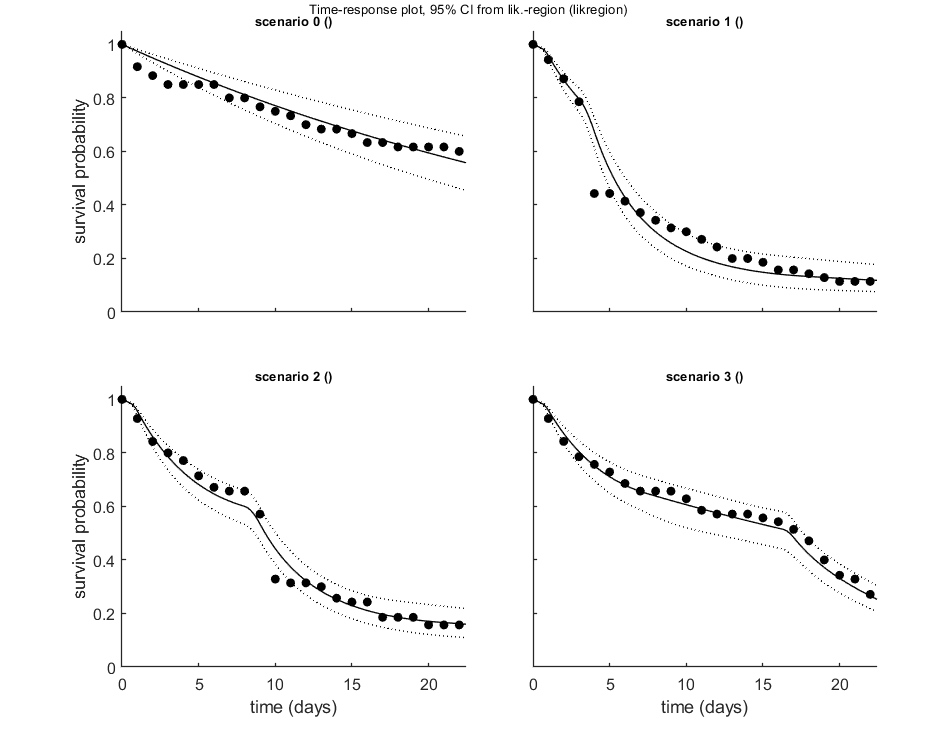
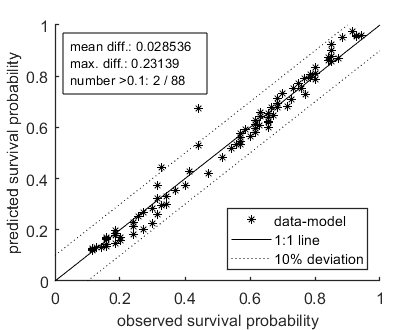
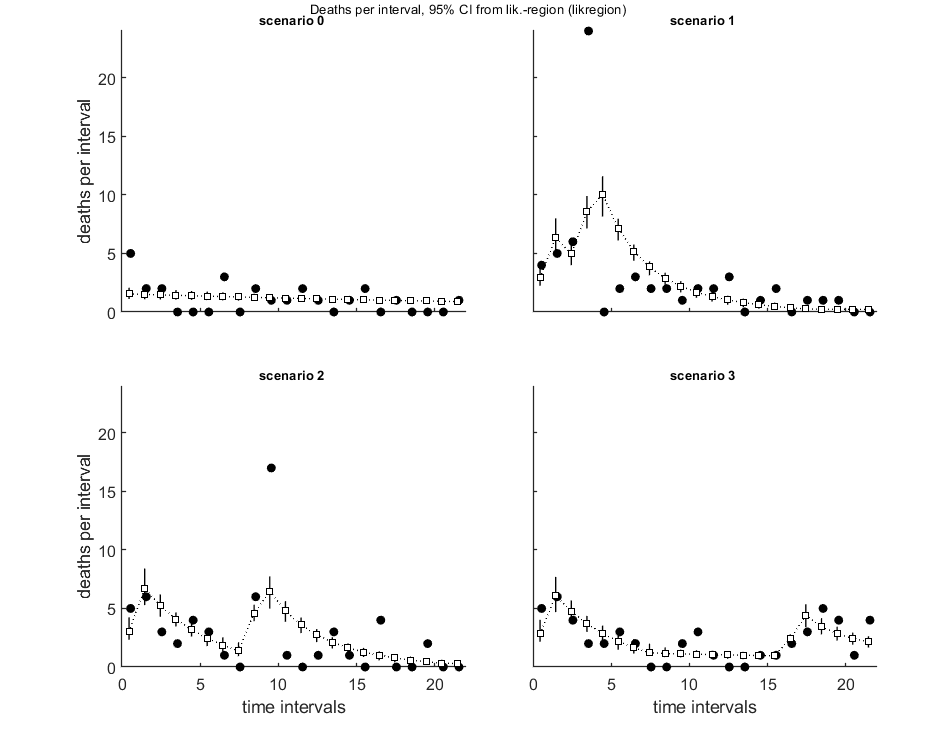
The following code can be used to make a standard plot (the same as for the fits), but with confidence intervals (and sampling error for survival data, if needed; Bayes only).
The plot_guts function makes multiplots for the survival data, which are more readable when plotting with various intervals.
opt_conf.type = 2; % use the values from the slice sampler (1) or likelihood region (2) to make intervals opt_conf.lim_set = 2; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE AND PLOT % Calculate and plot extra plots, specifically for GUTS. opt_guts.doseresp = 0; % set to zero as a dose-response is meaningless for time-var. exposure plot_guts(par_out,opt_conf,opt_guts);
Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 9 mins, 7.6 secs Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 9 mins, 8.6 secs ============================================================================ Test for goodness-of-fit (Pearson chi-square with MC simulated distribution). Observed fit is better than this fraction of samples (p-value): 0.001 Fit rejected at a=0.05; the data are not consistent with the calibrated model. ============================================================================
Calculate LPx
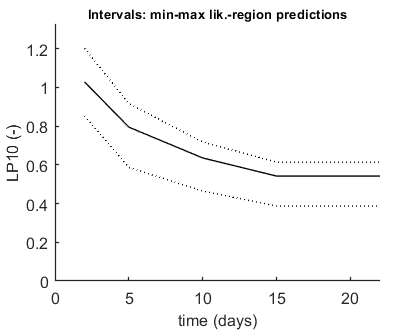
We can calculate an exposure multiplication factor: with which factor do we need to multiply an exposure scenario to obtain x% effect at the end of the scenario? Here, done for 10% effect after 2-22 days for scenario number 2 (as defined in the data set).
opt_conf.type = 2; % use the values from the slice sampler (1) or likelihood region (2) to make intervals opt_conf.lim_set = 2; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % this is the slow and general method that can work with a time vector opt_lc50.Feff = 0.10; % effect level (>0 en <1), x/100 in LCx opt_lc50.Fexp = [1 2]; % set first value to 1 to calculate exposure factor instead of LCx, second value is scenario identifier in X0mat Tend = [2 5 10 15 22]; % times at which to calculate exposure factor, relative to control calc_conf_lc50(par_out,Tend,opt_conf,opt_lc50); % calculates LPx values, CI requires that there is a mat file with sample % this is the new fast method that only does on t at a time opt_lpx.Feff = 0.10; % effect level (>0 en <1), x/100 in LCx opt_lpx.scen_type = 4; % type of definition for the exposure scenario (as used in make_scen) Tend = 22; % time at which to calculate exposure factor, relative to control (this function cannot work with a T vector!) calc_conf_lpx_lim(par_out,Tend,2,opt_conf,opt_lpx);
Calculate LPx for scenario 2 Note that first column in X0mat is used for starting values ================================================================================= LP10 ( 2 days): 1.029 LP10 ( 5 days): 0.7948 LP10 ( 10 days): 0.6357 LP10 ( 15 days): 0.5421 LP10 ( 22 days): 0.5421 ================================================================================= Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 ================================================================================= LP10 ( 2 days): 1.029 (0.8533-1.203) LP10 ( 5 days): 0.7948 (0.5868-0.9166) LP10 ( 10 days): 0.6357 (0.4649-0.7181) LP10 ( 15 days): 0.5421 (0.3874-0.6141) LP10 ( 22 days): 0.5421 (0.3874-0.6141) ================================================================================= Intervals: 95% confidence (likelihood region) Time required: 9 mins, 30.6 secs Calculate exposure multiplication factors ================================================================== LP10 ( 22 days): 0.5421 ================================================================== Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 Results table for LPx (-) with 95% CI, scenario 2 ================================================================== LP10 ( 22 days): 0.5421 (0.3873-0.6141) ================================================================== Intervals: 95% confidence (likelihood region) Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 9 mins, 31.5 secs Time required: 9 mins, 31.6 secs
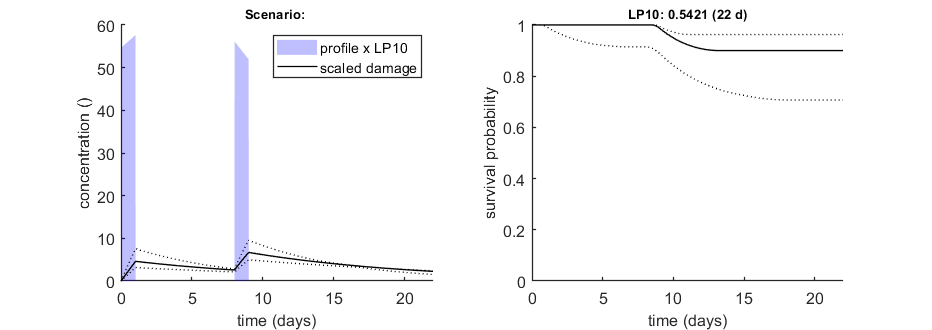
Calculate LCx versus time
Here, the LCx (by default the LC50) is calculated at several time points.
opt_conf.type = 2; % use the values from the slice sampler (1) or likelihood region (2) to make intervals opt_conf.lim_set = 2; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % We can directly use the fast method specific for this reduced GUTS folder opt_lcx.Feff = 0.50; % effect level (>0 en <1), x/100 in LCx Tend = [2:0.2:3 3.5 4:8 10 15 22]; % times at which to calculate LCx, relative to control calc_conf_lcx_lim(par_out,Tend,opt_conf,opt_lcx); % calculates LCx values, CI requires that there is a mat file with sample % We can also use the older slower version, but we need to remove all % scenario information first. We used pulsed exposure scenarios to fit the % parameters, but the LC50 calculations uses X0mat to transfer real % concentrations to the model, not scenario numbers (this might interfere % with previously defined scenarios). % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % make_scen(-5,-1); % remove all spline info from glo % opt_lc50.Feff = 0.50; % effect level (>0 en <1), x/100 in LCx % opt_lc50.Fexp = [0 2]; % turn off the calculation of the exposure factor, and move back to LCx % Tend = [2:0.2:3 3.5 4:8 10 15 22]; % times at which to calculate LCx, relative to control % calc_conf_lc50(par_out,Tend,opt_conf,opt_lc50); % calculates LCx values, CI requires that there is a mat file with sample
Calculate LCx values Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 240 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 Results table for LCx,t (), with 95% CI ================================================================== LC50 ( 2 days): 247.8 (200.2-333.3) LC50 ( 2.2 days): 210.3 (170.9-280.3) LC50 ( 2.4 days): 181.4 (148.2-239.6) LC50 ( 2.6 days): 158.5 (130.2-207.7) LC50 ( 2.8 days): 140.1 (115.7-182.1) LC50 ( 3 days): 125.1 (103.8-161.3) LC50 ( 3.5 days): 97.51 (81.81-123.4) LC50 ( 4 days): 79.01 (66.98-98.30) LC50 ( 5 days): 56.25 (48.59-67.99) LC50 ( 6 days): 43.14 (37.84-51.49) LC50 ( 7 days): 34.80 (30.77-41.06) LC50 ( 8 days): 29.10 (25.94-33.98) LC50 ( 10 days): 21.94 (19.81-25.16) LC50 ( 15 days): 13.93 (12.73-15.52) LC50 ( 22 days): 9.806 (8.452-11.14) ================================================================== Intervals: 95% confidence (likelihood region) Time required: 9 mins, 33.3 secs
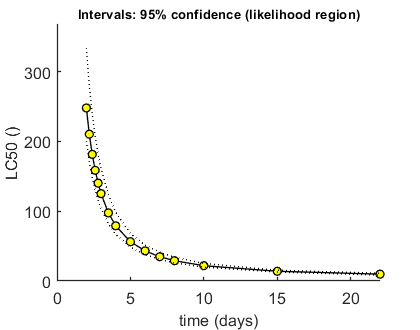
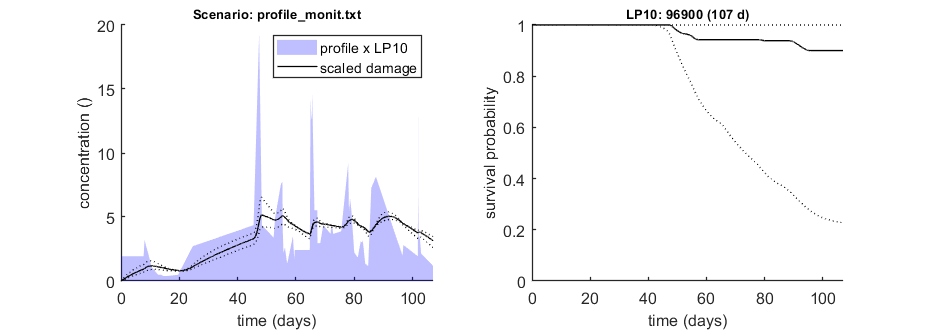
Calculate LPx for a monitoring profile
We can use the function calc_conf_lpx_lim to calculate an exposure multiplication factor: with which factor do we need to multiply an exposure scenario to obtain x% effect at the end of the scenario? Here, done for 10% effect at the end of the exposure scenario.
This is the fast method, which is closely linked to this GUTS model (reduced model, standard directory). Don't use if you modify the GUTS model in simplefun.m or derivatives.m, unless you know what you are doing. The function calc_conf_lc50 can also calculate LPx values. This works more generally, but much slower, and it requires some more tricked-out coding. Contact me if you feel the need to use it.
% UNCOMMENT FOLLOWING LINE(S) TO CALCULATE opt_conf.type = 2; % use values from slice sampler (1), likelihood region(2) to make intervals (-1 to skip intervals) opt_conf.lim_set = 1; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs opt_lpx.Feff = 0.10; % effect level (>0 en <1), x/100 in LCx opt_lpx.scen_type = 4; % type of definition for the exposure scenario (as used in make_scen) glo.useode = 0; % no need for ODE solver, as long as scen_type = 4 (linear forcing) Tend = []; % time at which to calculate LPx (empty is end of profile) LPx_mon = calc_conf_lpx_lim(par_out,Tend,'profile_monit.txt',opt_conf,opt_lpx);
Calculate exposure multiplication factors ================================================================== LP10 ( 107 days): 9.690e+04 ================================================================== Amount of 0.4 added to the chi-square criterion for inner rim Limited set of 200 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 Results table for LPx (-) with 95% CI, scenario 1 ================================================================== LP10 ( 107 days): 9.690e+04 (6.525e+04-1.188e+05) ================================================================== Intervals: 95% confidence (likelihood region) Amount of 0.4 added to the chi-square criterion for inner rim Limited set of 200 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 9 mins, 55.5 secs Time required: 9 mins, 55.5 secs