BYOM, byom_guts_extra.m
- Author: Tjalling Jager
- Date: September 2018
- Web support: http://www.debtox.info/byom.html
- Back to index walkthrough_guts.html
BYOM is a General framework for simulating model systems in terms of ordinary differential equations (ODEs). The model itself needs to be specified in derivatives.m or simplefun.m, and call_deri.m may need to be modified to the particular problem as well. The files in the engine directory are needed for fitting and plotting. Results are shown on screen but also saved to a log file (results.out).
The model: fitting survival data with the GUTS special cases based on the reduced model (TK and damage dynamics lumped): SD, IT and mixed (or GUTS proper). For faster calculations, scaled damage is calculated using the analytical solution in simplefun.m. To use the ODE version, set the option glo.useode= 1 (which uses the model in derivatives.m). Some types of time-varying exposure can use (partial) analytical solutions as well. Calculation of the death mechanisms (SD, IT and mixed) is done in call_deri.m.
The equation for scaled damage (referenced to water) is used both by SD and IT:
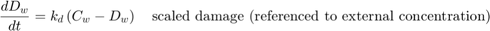
The SD model uses the hazard rate, which is calculated as:
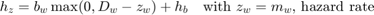
The hazard rate is integrated over time to yield the survival probability:
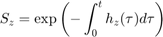
The IT model first finds the maximum of the scaled damage over time:
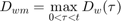
And then uses the cumulative distribution of the thresholds to find the survival probability:
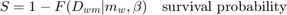
This script: Long acute toxicity test for guppy (Poecilia reticulata) exposed to the insecticide dieldrin. Data from: Bedaux and Kooijman (1994), http://dx.doi.org/10.1007/BF00469427. In this script, many options for post-calculations are provided. You can copy the parts of code that you need to the other examples (and your own analyses).
Contents
- Initial things
- The data set
- Initial values for the state variables
- Initial values for the model parameters
- Time vector and labels for plots
- Calculations and plotting
- Local sensitivity analysis
- Profiling the likelihood
- Slice sampler
- Likelihood region
- Plot results with confidence intervals
- Calculate LCx versus time
- Calculate LPx for a monitoring profile
- Other files: derivatives
- Other files: call_deri
Initial things
Make sure that this script is in a directory somewhere below the BYOM folder.
clear, clear global % clear the workspace and globals global DATA W X0mat % make the data set and initial states global variables global glo % allow for global parameters in structure glo global pri zvd % global structures for optional priors and zero-variate data diary off % turn of the diary function (if it is accidentaly on) % set(0,'DefaultFigureWindowStyle','docked'); % collect all figure into one window with tab controls set(0,'DefaultFigureWindowStyle','normal'); % separate figure windows pathdefine % set path to the BYOM/engine directory glo.basenm = mfilename; % remember the filename for THIS file for the plots glo.saveplt = 0; % save all plots as (1) Matlab figures, (2) JPEG file or (3) PDF (see all_options.txt)
The data set
Data are entered in matrix form, time in rows, scenarios (exposure concentrations) in columns. First column are the exposure times, first row are the concentrations or scenario numbers. The number in the top left of the matrix indicates how to calculate the likelihood:
- -1 for multinomial likelihood (for survival data)
- 0 for log-transform the data, then normal likelihood
- 0.5 for square-root transform the data, then normal likelihood
- 1 for no transformation of the data, then normal likelihood
% observed number of survivors, time in days, conc. in ug/L DATA{1} = [ -1 0 3.2 5.6 10 18 32 56 100 0 20 20 20 20 20 20 20 20 1 20 20 20 20 18 18 17 5 2 20 20 19 17 15 9 6 0 3 20 20 19 15 9 2 1 0 4 20 20 19 14 4 1 0 0 5 20 20 18 12 4 0 0 0 6 20 19 18 9 3 0 0 0 7 20 18 18 8 2 0 0 0 ]; % % demonstration of how static-renewal can be used in BYOM % Cw = [ -1 3.2 5.6 10 18 32 56 100 % these are now the scenario identifiers % 0 3.2 5.6 10 18 32 56 100 % initial concentrations at t=0 % 2 3.2 5.6 10 18 32 56 100 % renewals at t=2 % 4 3.2 5.6 10 18 32 56 100 % renewals at t=4 % 6 3.2 5.6 10 18 32 56 100 % renewals at t=6 % 7 0.2 0.2 0.2 0.2 0.2 0.2 0.2]; % last time point and disappearance rate constant for each scenario % % make_scen(3,Cw); % create the global definition for the exposure scenarios in Cw % Note: For survival data, the weights matrix W has a different meaning % than for continuous data: it can be used to specify the number of animals % that went missing or were removed during the experiment (enter the number % of missing/removed animals at the time they were last seen alive in the % test). By default, the weights matrix for survival data is filled with % zeros. % scaled damage, can have no observations DATA{2} = 0;
Initial values for the state variables
Initial states, scenarios in columns, states in rows. First row are the 'names' of all scenarios.
X0mat(1,:) = DATA{1}(1,2:end); % scenarios (concentrations)
X0mat(2,:) = 1; % initial survival probability
X0mat(3,:) = 0; % initial scaled damage
Initial values for the model parameters
Model parameters are part of a 'structure' for easy reference.
% global parameters for GUTS purposes glo.sel = 1; % select death mechanism: 1) SD 2) IT 3) mixed glo.locD = 2; % location of scaled damage in the state variable list glo.locS = 1; % location of survival probability in the state variable list % start values for SD % syntax: par.name = [startvalue fit(0/1) minval maxval optional:log/normal scale (0/1)]; par.kd = [0.5 1 1e-3 100 0]; % dominant rate constant, d-1 par.mw = [5 1 0 1e6 1]; % median threshold for survival (ug/L) par.hb = [0.01 1 0 1 1]; % background hazard rate (1/d) par.bw = [0.05 1 1e-6 1e6 0]; % killing rate (L/ug/d) (SD only) par.Fs = [3 1 1 100 1]; % fraction spread of threshold distribution (IT only) % % start values for IT % % syntax: par.name = [startvalue fit(0/1) minval maxval optional:log/normal scale (0/1)]; % par.kd = [0.008 1 1e-3 100 0]; % dominant rate constant (d-1) % par.mw = [0.5 1 0 1e6 1]; % median threshold for survival (ug/L) % par.hb = [0.001 1 0 1 1]; % background hazard rate (1/d) % par.bw = [0.04 1 1e-6 1e6 0]; % killing rate (L/ug/d) (SD and mixed) % par.Fs = [3.8 1 1 100 1]; % fraction spread of NEC distribution (-) (IT and mixed) switch glo.sel % make sure that right parameters are fitted case 1 % for SD ... par.Fs(2) = 0; % never fit the threshold spread! case 2 % for IT ... par.bw(2) = 0; % never fit the killing rate! case 3 % mixed % do nothing: fit all parameters end
Time vector and labels for plots
Specify what to plot. If time vector glo.t is not specified, a default is used, based on the data set
% specify the y-axis labels for each state variable glo.ylab{1} = 'survival probability'; glo.ylab{2} = ['scaled damage (',char(181),'g/L)']; % specify the x-axis label (same for all states) glo.xlab = 'time (days)'; glo.leglab1 = 'conc. '; % legend label before the 'scenario' number glo.leglab2 = [char(181),'g/L']; % legend label after the 'scenario' number prelim_checks % script to perform some preliminary checks and set things up % Note: prelim_checks also fills all the options (opt_...) with defauls, so % modify options after this call, if needed.
Calculations and plotting
Here, the function is called that will do the calculation and the plotting. Options for the plotting can be set using opt_plot (see prelim_checks.m). Options for the optimisation routine can be set using opt_optim. Options for the ODE solver are part of the global glo.
For the demo, the iterations are turned off (opt_optim.it = 0).
glo.useode = 0; % calculate model using ODE solver (1) or analytical solution (0) if glo.sel == 1 % for the pure SD model, turn on the events function to catch threshold exceedance glo.eventson = 1; % events function on (1) or off (0) end % par = start_vals_guts(par); % experimental start-value finder; use at your own risk % % Note: start_vals will now overwrite the parameter structure par! % glo.fastslow = 's'; % tell simplefun that we need slow (s) or fast (f) kinetics, (o) is off (default) % par.kd(2) = 0; % don't fit the dominant rate constant anymore % % slow kinetics implies that mw is now used for mw/kd and bw becomes bw*kd! % par.mw = [60 1 0 1e6 1]; % median threshold-time for survival (d ug/L) % % here, I only define a new starting value for mw/kd, assuming we're fitting IT opt_optim.fit = 1; % fit the parameters (1), or don't (0) opt_optim.it = 0; % show iterations of the optimisation (1, default) or not (0) opt_plot.bw = 1; % if set to 1, plots in black and white with different plot symbols opt_plot.annot = 2; % annotations in multiplot for fits: 1) box with parameter estimates 2) single legend % opt_plot.statsup = [2]; % vector with states to suppress in plotting fits % optimise and plot (fitted parameters in par_out) par_out = calc_optim(par,opt_optim); % start the optimisation calc_and_plot(par_out,opt_plot); % calculate model lines and plot them % plot_guts(par_out,[],opt_guts); % uncomment to make more detailed GUTS plots (without CIs) % savenm = 'fit_dieldrin'; % file name to save a plot ad hoc % save_plot(gcf,savenm,[],3) % save active figure as PDF (see save_plot for more options) % print_par(par_out) % print fitted parameters on-screen in format that can be copied into this script
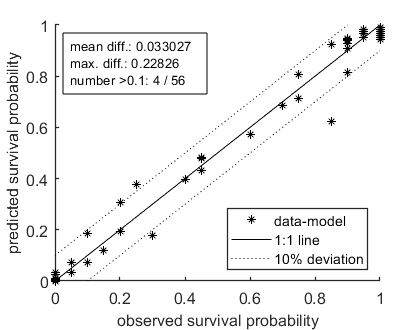
Goodness-of-fit measures for each data set (R-square)
0.9869
Warning: R-square is not appropriate for survival data and needs to be
interpreted more qualitatively!
=================================================================================
Results of the parameter estimation with BYOM version 4.2b
=================================================================================
Filename : byom_guts_extra
Analysis date : 06-Sep-2018 (15:37)
Data entered :
data state 1: 8x8, survival data.
data state 2: 0x0, no data.
Search method: Nelder-Mead simplex direct search, 2 rounds.
The optimisation routine has converged to a solution
Total 146 simplex iterations used to optimise.
Minus log-likelihood has reached the value 161.527 (AIC=331.053).
=================================================================================
kd 0.791 (fit: 1, initial: 0.5)
mw 5.205 (fit: 1, initial: 5)
hb 0.008353 (fit: 1, initial: 0.01)
bw 0.03761 (fit: 1, initial: 0.05)
Fs 3 (fit: 0, initial: 3)
=================================================================================
Parameters kd and bw are fitted on log-scale.
=================================================================================
Time required: 0.6 secs
Plots result from the optimised parameter values.
Local sensitivity analysis
Local sensitivity analysis of the model. All model parameters are increased one-by-one by a small percentage. The sensitivity score is by default scaled (dX/X p/dp) or alternatively absolute (dX p/dp).
Options for the sensitivity can be set using opt_sense (see prelim_checks.m).
% % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % calc_localsens(par_out,opt_sens)
Profiling the likelihood
By profiling you make robust confidence intervals for one or more of your parameters. Use the name of the parameter as it occurs in your parameter structure par above. You do not need to run the entire script before you can make a profile.
Options for the profiling can be set using opt_prof (see prelim_checks). For this demo, no sub-optimisations are used. However, consider this options when working on your own data (e.g., set opt_prof.subopt=10).
The level of detail of the profiling is set to 'detailed' for this demo to catch the local optimum (it is just within the 95% CI, which is thus a broken set)
opt_prof.detail = 1; % detailed (1) or a coarse (2) calculation opt_prof.subopt = 0; % number of sub-optimisations to perform to increase robustness % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % run a profile for selected parameters ... % calc_proflik(par_out,'kd',opt_prof); % calculate a profile % calc_proflik(par_out,'mw',opt_prof); % calculate a profile % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % % Automatically calculate profiles for all parameters, and redo % % optimisation when a better value is found. % opt_prof.subopt = -1; % number of sub-optimisations to perform to increase robustness % % Note: a -1 here makes a comparison between 0 and 10 sub-optimisations. % % In this example, sub-optimisations are helpful! % par_out = auto_profiles(par_out,opt_prof,opt_optim);
Slice sampler
The slice sampler can be used for a Bayesian analysis as it provides a sample from the posterior distribution. A .mat file is saved which contains the sample, to use later for e.g., intervals on model predictions. The output includes the Markov chain and marginal distributions for each fitted parameter. The function calc_conf can be used to put confidence intervals on the model lines.
Options for the slice sampling can be set using opt_slice (see prelim_checks). Options for confidence bounds on model curves and calculation of error ellipse can be set using opt_conf (see prelim_checks).
For this data set, it is difficult to obtain a proper posterior (one that can be integrated so that sample can be normalised to a prob. density function). For SD, hb runs towards zero, and for IT, kd runs to zero. Some careful selection of priors will be needed to make the posterior proper. Therefore, this analysis is skipped here, and only the likelihood-region method is used.
% % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE % opt_slice.thin = 25; % thinning of the sample (keep one in every 'thin' samples) % opt_slice.burn = 200; % number of burn-in samples (0 is no burn in) % opt_slice.alllog = 1; % set to 1 to put all parameters on log-scale before taking the sample % % calc_slice(par_out,1000,opt_slice); % second argument number of samples (-1 to re-use saved sample from previous runs)
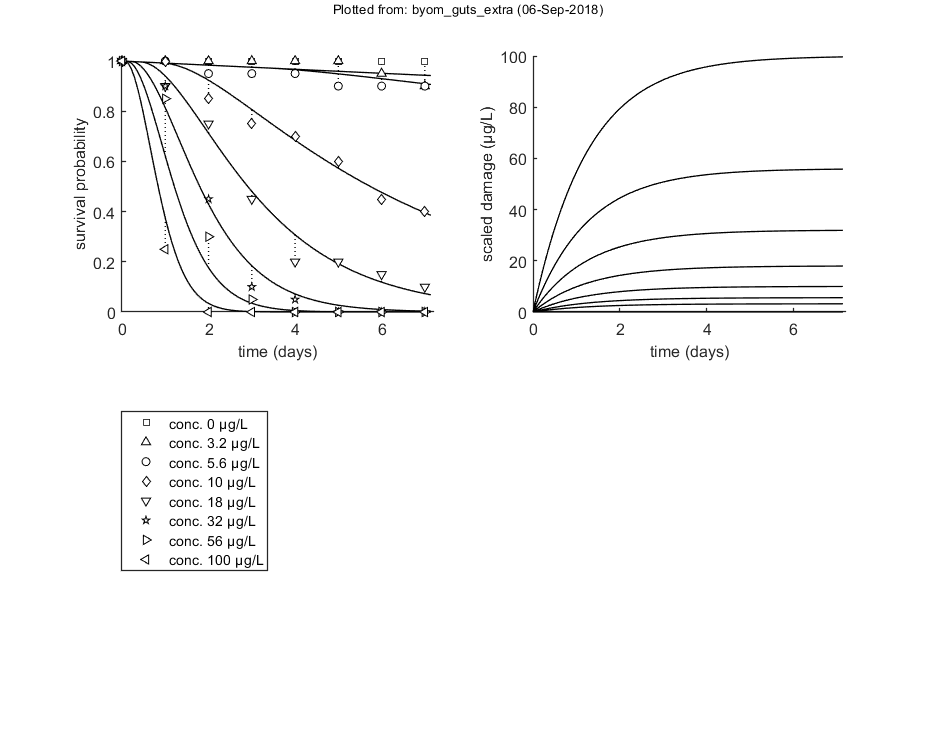
Likelihood region
Another way to make intervals on model predictions is to use a sample of parameter sets taken from the joint likelihood-based conf. region. This is done by the function calc_likregion.m. It first does profiling of all fitted parameters to find the edges of the region. Then, Latin-Hypercube sampling, keeping only those parameter combinations that are not rejected at the 95% level in a lik.-rat. test. The inner rim will be used for CIs on forward predictions.
Options for the likelihood region can be set using opt_likreg (see prelim_checks.m).
% UNCOMMENT FOLLOWING LINE(S) TO CALCULATE opt_likreg.subopt = 10; % number of sub-optimisations to perform to increase robustness opt_likreg.detail = 1; % detailed (1) or a coarse (2) calculation opt_likreg.burst = 2000; % number of random sets from parameter space evaluated every iteration opt_likreg.skipprof = 0; % skip profiling step (1); use boundaries from saved set in MAT file from previous analysis calc_likregion(par_out,500,opt_likreg); % second argument: nr sets in inner region (-1 to re-use saved sample from previous runs)
Calculating profiles and sample from confidence region ... please be patient. Confidence interval from the profile (single parameter, 95% confidence) ================================================================================= kd interval: 0.4923 - 1.317 The confidence interval is a broken set (check likelihood profile to check these figures) mw interval: interval 1: 2.716 - 2.827 interval 2: 4.095 - 6.912 Warning: taking the lowest parameter value as lower confidence limit The confidence interval is a broken set (check likelihood profile to check these figures) hb interval: interval 1: 0 - 0.0001385 interval 2: 0.002105 - 0.02163 bw interval: 0.0263 - 0.05424 Edges of the joint 95% confidence region (using df=p) ================================================================================= kd interval: 0.3631 - 1.919 mw interval: 1.87 - 7.908 hb interval: 0 - 0.03208 bw interval: 0.01955 - 0.06864 Starting with obtaining a sample from the joint confidence region. Bursts of 2000 samples, until at least 500 samples are accepted in inner rim. Currently accepted (inner rim): 0, 18, 32, 58, 78, 93, 112, 130, 149, 176, 197, 221, 244, 261, 283, 295, 310, 326, 344, 363, 382, 408, 424, 443, 463, 483, Size of total sample (profile points have been added): 52207 of which accepted in the conf. region: 4418, and in inner rim: 623 Time required: 10 mins, 51.5 secs
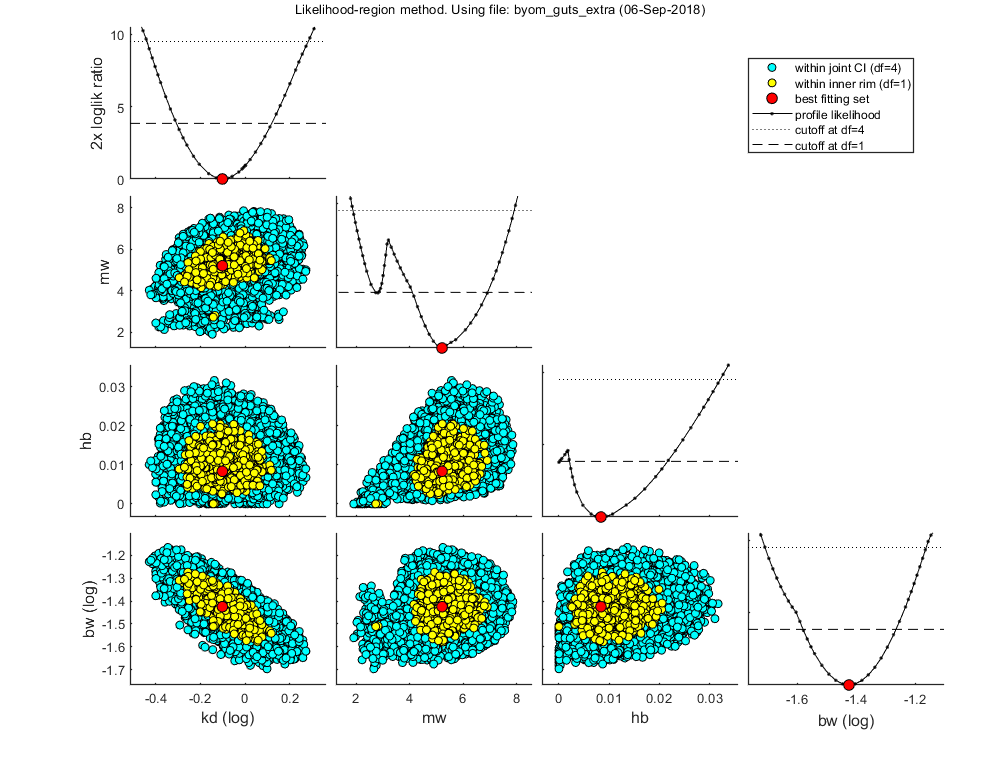
Plot results with confidence intervals
The following code can be used to make a standard plot (the same as for the fits), but with confidence intervals, and sampling error for survival data, if needed. Sampling error is restricted to Bayesian analyses for the moment (for likelihood region, it needs more work). Options for confidence bounds on model curves can be set using opt_conf (see prelim_checks).
Use opt_conf.type to tell calc_conf which sample to use: 1) Bayesian MCMC sample (default); CI on predictions are 95% ranges on the model curves from the sample 2) parameter sets from a joint likelihood region (limited sets can be used), which will yield (asymptotically) 95% CIs on predictions
The plot_guts function makes multiplots for the survival data, which are more readable when plotting with various intervals. Plot_guts plots survival vs. time, survival vs. concentration, and deaths per time interval. Note that plot_guts calls calc_conf itself, so there is no need to run it here first to obtain out_conf. The options opt_conf are also used by plot_guts. Leave them as empty matrix to suppress all CIs for the GUTS plots.
opt_conf.type = 2; % use the values from the slice sampler (1) or likelihood region (2) to make intervals opt_conf.lim_set = 0; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs % % UNCOMMENT FOLLOWING LINE(S) TO CALCULATE AND PLOT % out_conf = calc_conf(par_out,opt_conf,opt_plot.repls); % calculate confidence intervals on model curves % % Note: extra argument opt_plot.repls is needed to obtain correct sampling error (so when opt_conf.samerr = 1, and Bayes only). % calc_and_plot(par_out,opt_plot,out_conf); % call the plotting routine again to make fits with CIs (not so readable) % Calculate and plot extra plots, specifically for GUTS. These plots are % more readable when plotting CIs. plot_guts(par_out,opt_conf,opt_guts);
Amount of 0.4 added to the chi-square criterion for inner rim Full sample of 749 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 10 mins, 53.7 secs Amount of 0.4 added to the chi-square criterion for inner rim Full sample of 749 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 10 mins, 55.9 secs ============================================================================ Test for goodness-of-fit (Pearson chi-square with MC simulated distribution). Observed fit is better than this fraction of samples (p-value): 0.7676 Fit is not rejected at a=0.05. ============================================================================ Amount of 0.4 added to the chi-square criterion for inner rim Full sample of 749 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 11 mins, 5.0 secs
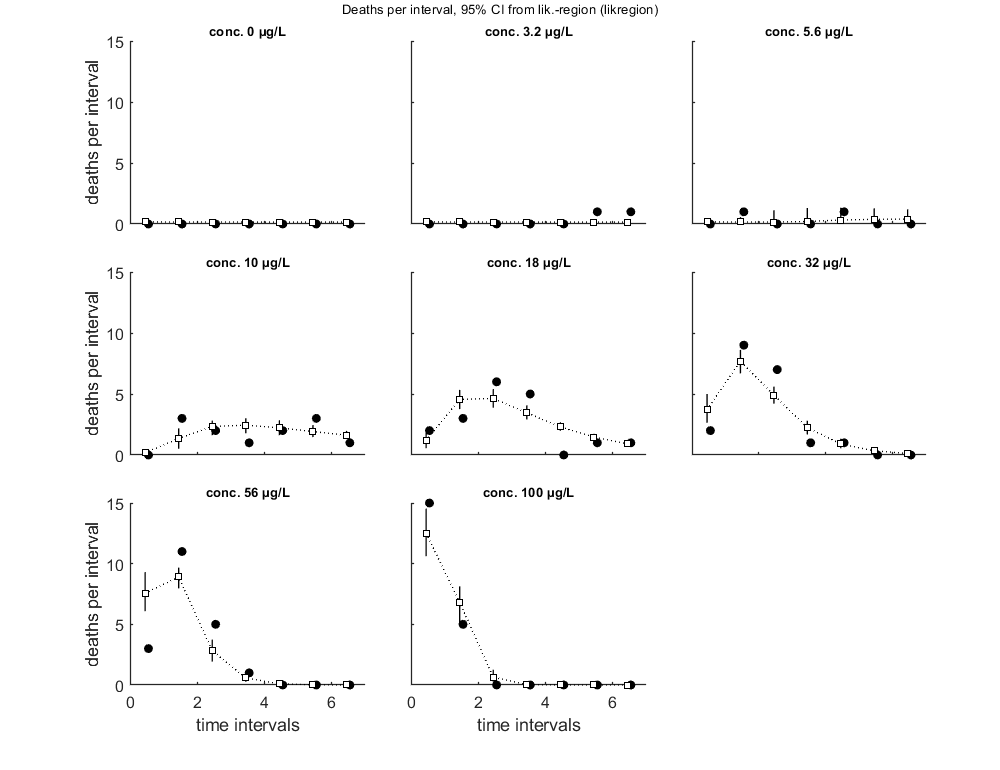
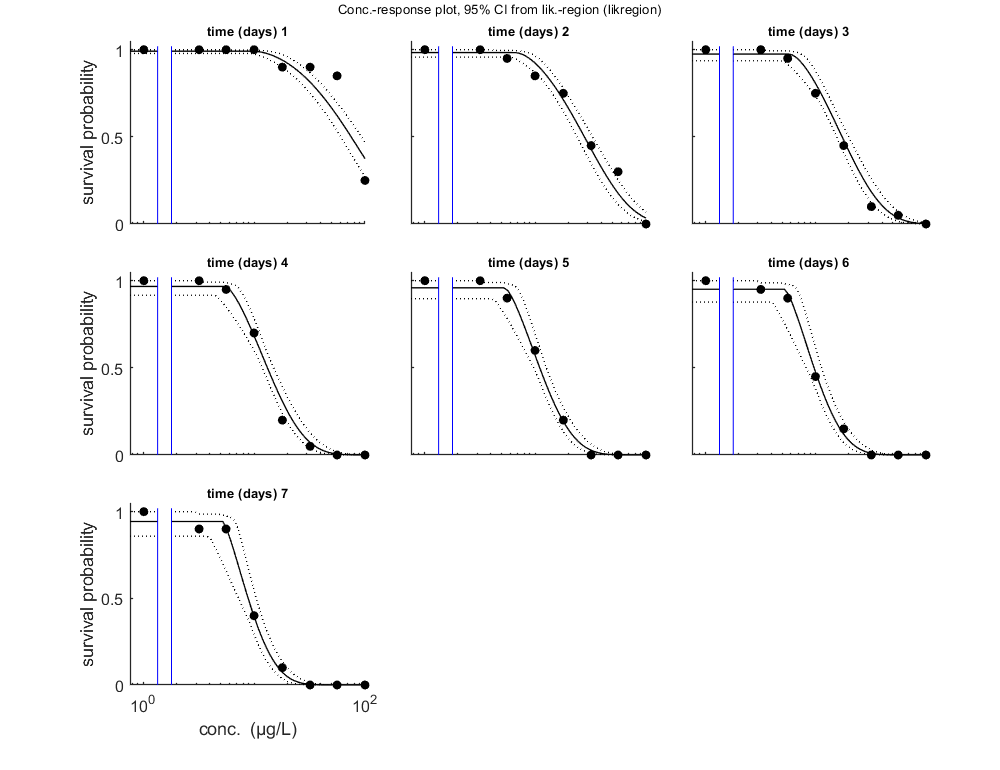
Calculate LCx versus time
Here, the LCx (by default the LC50) is calculated at several time points. When sufficient points are specified, a smooth line for LCx versus time will be produced. LCx values are also printed on screen. If a sample from parameter space is available (either from the slice sampler or the likelihood region), it can be used to calculate confidence bounds.
Here, a faster method is used with calc_conf_lcx_lim, which only works with the standard models as provided in this package (and in this case only the reduced model). As soon as you modify the model (in call_deri, derivatives or simplefun) it will likely produce erroneous results. The function calc_conf_lc50 is more generally applicable.
Options for LCx (with confidence bounds) can be set using opt_lcx (see prelim_checks). Note that the calculations assume initial values for each state as defined in the first column if X0mat!
% UNCOMMENT FOLLOWING LINE(S) TO CALCULATE opt_conf.type = 2; % use the values from the slice sampler (1) or likelihood region (2) to make intervals opt_conf.lim_set = 0; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs Tend = [1:0.2:3 3.5 4:8]; % times at which to calculate LCx, relative to control calc_conf_lcx_lim(par_out,Tend,opt_conf,opt_lcx); % calculates LCx values, CI requires that there is a mat file with sample % calc_conf_lc50(par_out,Tend,opt_conf,opt_lc50); % slow method to calculate LCx values
Calculate LCx values Amount of 0.4 added to the chi-square criterion for inner rim Full sample of 749 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 Results table for LCx,t (µg/L), with 95% CI ================================================================== LC50 ( 1 days): 75.74 (61.05-93.70) LC50 ( 1.2 days): 57.32 (46.82-70.18) LC50 ( 1.4 days): 45.76 (37.84-55.49) LC50 ( 1.6 days): 37.96 (31.76-45.62) LC50 ( 1.8 days): 32.42 (27.42-38.63) LC50 ( 2 days): 28.32 (24.19-33.47) LC50 ( 2.2 days): 25.18 (21.72-29.54) LC50 ( 2.4 days): 22.71 (19.77-26.46) LC50 ( 2.6 days): 20.74 (18.20-24.00) LC50 ( 2.8 days): 19.13 (16.92-21.99) LC50 ( 3 days): 17.79 (15.85-20.33) LC50 ( 3.5 days): 15.28 (13.76-17.41) LC50 ( 4 days): 13.55 (12.21-15.43) LC50 ( 5 days): 11.34 (9.731-13.13) LC50 ( 6 days): 10.01 (8.232-11.75) LC50 ( 7 days): 9.141 (7.245-10.83) LC50 ( 8 days): 8.526 (6.551-10.18) ================================================================== Intervals: 95% confidence (likelihood region) Time required: 11 mins, 10.6 secs
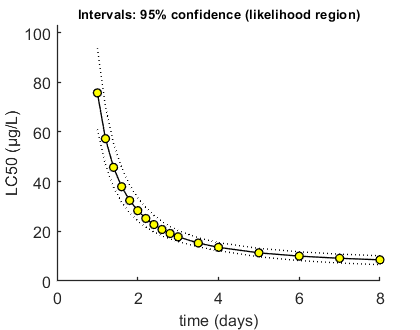
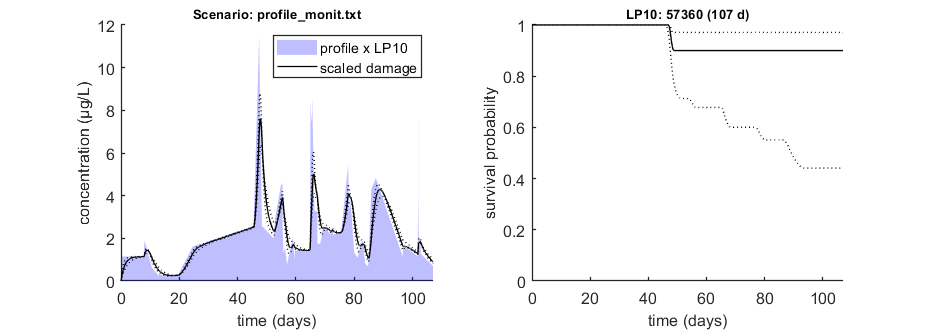
Calculate LPx for a monitoring profile
We can use the function calc_conf_lpx_lim to calculate an exposure multiplication factor: with which factor do we need to multiply an exposure scenario to obtain x% effect at the end of the scenario? Here, done for 10% effect at the end of the exposure scenario.
This is the fast method, which is closely linked to this GUTS model (reduced model, standard directory). Don't use if you modify the GUTS model in simplefun.m, call_deri.m or derivatives.m, unless you know what you are doing. The function calc_conf_lc50 can also calculate LPx values. That function works more generally, but much slower, and it requires some more tricked-out coding. Contact me if you feel the need to use it.
% UNCOMMENT FOLLOWING LINE(S) TO CALCULATE opt_conf.type = 2; % use values from slice sampler (1), likelihood region(2) to make intervals (-1 to skip intervals) opt_conf.lim_set = 2; % for lik-region sample: use limited set of n_lim points (1) or outer hull (2) to create CIs opt_lpx.Feff = 0.10; % effect level (>0 en <1), x/100 in LCx glo.useode = 0; % no need for ODE solver, as long as scen_type = 4 (default, linear forcing) Tend = []; % time at which to calculate LPx (empty is end of profile) LPx_mon = calc_conf_lpx_lim(par_out,Tend,'profile_monit.txt',opt_conf,opt_lpx);
Calculate exposure multiplication factors ================================================================== LP10 ( 107 days): 5.736e+04 ================================================================== Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 251 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of sets finished for CIs: 0 10 20 30 40 50 60 70 80 90 Results table for LPx (-) with 95% CI, scenario 1 ================================================================== LP10 ( 107 days): 5.736e+04 (3.692e+04-6.856e+04) ================================================================== Intervals: 95% confidence (likelihood region) Amount of 0.4 added to the chi-square criterion for inner rim Outer hull of 251 sets used. Calculating CIs on model predictions, using sample from joint likelihood region ... please be patient. Percentage of samples finished: 0 10 20 30 40 50 60 70 80 90 Time required: 11 mins, 37.8 secs Time required: 11 mins, 37.8 secs
Other files: derivatives
To archive analyses, publishing them with Matlab is convenient. To keep track of what was done, the file derivatives.m can be included in the published result.
%% BYOM function derivatives.m (the model in ODEs) % % Syntax: dX = derivatives(t,X,par,c) % % This function calculates the derivatives for the reduced GUTS model % system. Note that the survival probability due to chemical stress is all % calculated in <call_deri.html call_deri.m>. As input, it gets: % % * _t_ is the time point, provided by the ODE solver % * _X_ is a vector with the previous value of the states % * _par_ is the parameter structure % * _c_ is the external concentration (or scenario number) % % Time _t_ and scenario name _c_ are handed over as single numbers by % <call_deri.html call_deri.m> (you do not have to use them in this % function). Output _dX_ (as vector) provides the differentials for each % state at _t_. % % * Author: Tjalling Jager % * Date: September 2018 % * Web support: <http://www.debtox.info/byom.html> % * Back to index <walkthrough_guts.html> %% Start function dX = derivatives(t,X,par,c) global glo % allow for global parameters in structure glo (handy for switches) %% Unpack states % The state variables enter this function in the vector _X_. Here, we give % them a more handy name. S = X(1); % state 1 is the survival probability at previous time point Dw = X(2); % state 2 is the scaled damage at previous time point %% Unpack parameters % The parameters enter this function in the structure _par_. The names in % the structure are the same as those defined in the byom script file. % The 1 between parentheses is needed as each parameter has 5 associated % values. kd = par.kd(1); % dominant rate constant % mw = par.mw(1); % median of threshold distribution (used in call_deri) % bw = par.bw(1); % killing rate (used in call_deri) % Fs = par.Fs(1); % fraction spread of threshold distribution, (-) (used in call_deri) hb = par.hb(1); % background hazard rate %% Extract correct exposure for THIS time point % Allow for external concentrations to change over time, either % continuously, or in steps, or as a static renewal with first-order % disappearance. For constant exposure, the code in this section is skipped % (and could also be removed). if isfield(glo,'int_scen') % if it exists: use it to derive current external conc. if ismember(c,glo.int_scen) % is c in the scenario range global? c = make_scen(-1,c,t); % use make_scen again to derive actual exposure concentration % the -1 lets make_scen know we are calling from derivatives (so need one c) end end %% Calculate the derivatives % This is the actual model, specified as a system of ODEs. dDw = kd * (c - Dw); % first order damage build-up from c (scaled) dS = -hb* S; % only background hazard rate % mortality due to the chemical is included in call_deri! dX = [dS;dDw]; % collect derivatives in one vector
Other files: call_deri
To archive analyses, publishing them with Matlab is convenient. To keep track of what was done, the file call_deri.m can be included in the published result.
%% BYOM function call_deri.m (calculates the model output) % % Syntax: [Xout TE] = call_deri(t,par,X0v) % % This function calls the ODE solver to solve the system of differential % equations specified in <derivatives.html derivatives.m>, or the explicit % function(s) in <simplefun.html simplefun.m>. As input, it gets: % % * _t_ the time vector % * _par_ the parameter structure % * _X0v_ a vector with initial states and one concentration (scenario number) % % The output _Xout_ provides a matrix with time in rows, and states in % columns. This function calls <derivatives.html derivatives.m> or % <simplefun.html simplefun.m>. The optional output _TE_ is the time at % which an event takes place (specified using the events function). The % events function is set up to catch discontinuities. It should be % specified according to the problem you are simulating. If you want to use % parameters that are (or influence) initial states, they have to be % included in this function. % % This function is for the reduced GUTS model. The external function % derivatives or simplefun provides the scaled damage over time and the % background mortality. Mortality due to chemical stress is calculated in % this function as a form of 'output mapping'. % % * Author: Tjalling Jager % * Date: September 2018 % * Web support: <http://www.debtox.info/byom.html> % * Back to index <walkthrough_guts.html> %% Start function [Xout,TE] = call_deri(t,par,X0v) global glo % allow for global parameters in structure glo global zvd % global structure for zero-variate data %% Initial settings % This part extracts optional settings for the ODE solver that can be set % in the main script (defaults are set in prelim_checks). The useode option % decides whether to calculate the model results using the ODEs in % <derivatives.html derivatives.m>, or the analytical solution in % <simplefun.html simplefun.m>. Using _eventson=1_ turns on the events % handling. Also modify the sub-function at the bottom of this function! % Further in this section, initial values can be determined by a parameter % (overwrite parts of _X0_), and zero-variate data can be calculated. See % the example BYOM files for more information. useode = glo.useode; % calculate model using ODE solver (1) or analytical solution (0) eventson = glo.eventson; % events function on (1) or off (0) stiff = glo.stiff; % set to 1 or 2 to use a stiff solver instead of the standard one min_t = 500; % minimum length of time vector (affects ODE stepsize as well) % Unpack the vector X0v, which is X0mat for one scenario X0 = X0v(2:end); % these are the intitial states for a scenario %% Calculations % This part calls the ODE solver (or the explicit model in <simplefun.html % simplefun.m>) to calculate the output (the value of the state variables % over time). There is generally no need to modify this part. The solver % ode45 generally works well. For stiff problems, the solver might become % very slow; you can try ode113 or ode15s instead. c = X0v(1); % the concentration (or scenario number) t = t(:); % force t to be a row vector (needed when useode=0) t_rem = t; % remember the original time vector (as we will add to it) options = odeset; % start with default options for the ODE solver % options = odeset(options, 'RelTol',1e-5,'AbsTol',1e-8); % specify tightened tolerances if isfield(glo,'int_scen') && ismember(c,glo.int_scen) % is c in the scenario range global? % then we have a time-varying concentration Tev = make_scen(-2,c,-1); % use make_scen again to derive actual exposure concentration % the -2 lets make_scen know we need events, the -1 that this is also needed for splines! min_t = max(min_t,length(Tev(Tev(:,1)<t(end),1))*2); % For very long exposure profiles (e.g., FOCUS profiles), we now % automatically generate a larger time vector (twice the number of the % relevant points in the scenario). options = odeset(options,'InitialStep',t_rem(end)/(10*min_t),'MaxStep',t_rem(end)/min_t); % For the ODE solver, when we have a time-varying exposure set here, we % base minimum step size on min_t. Small stepsize is a good idea for % pulsed exposures; otherwise, stepsize may become so large that a % concentration change is missed completely. else % options = odeset(options,'InitialStep',max(t)/100,'MaxStep',max(t)/10); % specify smaller stepsize % for constant concentrations, we can use a default or we can remove this option alltogether! % Matlab uses as default the length of the time vector divided by 10. end % For the GUTS cases, we need a long time vector. For the hazard and proper % model, we need to numerically integrate the hazard rate over time. For IT % in reduced models, we could make shortcuts, but since we don't know how % people may modify the models in derivatives or simplefun, it is better to % be general here. If the time span of the data set or simulation is very % long (and the number of points in Tev is not), consider increasing the % size of min_t. if length(t) < min_t % make sure there are at least min_t points t = unique([t;(linspace(t(1),t(end),min_t))']); end TE = 0; % dummy for time of events if useode == 1 % use the ODE solver to calculate the solution if eventson == 0 % if no events function is used ... switch stiff case 0 [~,Xout] = ode45(@derivatives,t,X0,options,par,c); case 1 [~,Xout] = ode113(@derivatives,t,X0,options,par,c); case 2 [~,Xout] = ode15s(@derivatives,t,X0,options,par,c); end else % with an events functions ... additional output arguments for events: % TE catches the time of an event, YE the states at the event, and IE the number of the event options = odeset(options, 'Events',@eventsfun); % add an events function switch stiff % note that YE and IE can be added as additional outputs case 0 [~,Xout,TE,~,~] = ode45(@derivatives,t,X0,options,par,c); case 1 [~,Xout,TE,~,~] = ode113(@derivatives,t,X0,options,par,c); case 2 [~,Xout,TE,~,~] = ode15s(@derivatives,t,X0,options,par,c); end end Xout = max(0,Xout); % in extreme cases, states can become ever so slightly negative else % alternatively, use an explicit function provided in simplefun! Xout = simplefun(t,X0,par,c); end if isempty(TE) || all(TE == 0) % if there is no event caught TE = +inf; % return infinity end %% Output mapping % _Xout_ contains a row for each state variable. It can be mapped to the % data. If you need to transform the model values to match the data, do it % here. % % This set of files is geared towards the use of the analytical solution % for the damage level in simplefun (although it can also be used with the % ODEs in derivatives). Therefore, only the damage level and background % survival is available at this point, and the survival due to the chemical % is added for each death mechanism below. mw = par.mw(1); % median of threshold distribution bw = par.bw(1); % killing rate Fs = max(1+1e-6,par.Fs(1)); % fraction spread of the threshold distribution beta = log(39)/log(Fs); % shape parameter for logistic from Fs S = Xout(:,glo.locS); % take background survival from the model Dw = Xout(:,glo.locD); % take the correct state variable for scaled damage switch glo.sel case 1 % stochastic death haz = bw * max(0,Dw-mw); % calculate hazard for each time point cumhaz = cumtrapz(t,haz); % integrate the hazard rate numerically S = S .* min(1,exp(-1*cumhaz)); % calculate survival probability, incl. background case 2 % individual tolerance, log-logistic distribution is used mw = max(mw,1e-100); % make sure that the threshold is not exactly zero ... % New method to make sure that Dw does not decrease over time (dead % animals dont become alive). This increases speed, especially when % there is very little decrease in Dw. maxDw = Dw; % copy the vector Dw to maxDw ind = find([0;diff(maxDw)]<0,1,'first'); % first index to places where Dw has decreased while ~isempty(ind) % as long as there is a decrease somewhere ... maxDw(ind:end) = max(maxDw(ind:end),maxDw(ind-1)); % replace every later time with max of that and previous point ind = find([0;diff(maxDw)]<0,1,'first'); % any decrease left? end S = S .* (1 ./ (1+(maxDw/mw).^beta)); % survival probability % the survival due to the chemical is multiplied with the background survival case 3 % mixed model % This is a fast way for GUTS proper. Damage is calculated only % once, as it is the same for all individuals. Survival for % different NECs is calculated below. n = 200; % number of slices from the threshold distribution Fs2 = 999^(1/beta); % fraction spread for 99.9% of the distribution z_range = linspace(mw/(1.5*Fs2),mw*Fs2,n); % range of NECs to cover 99.9% prob_range = ((beta/mw)*(z_range/mw).^(beta-1)) ./ ((1+(z_range/mw).^beta).^2); % pdf for the log-logistic (Wikipedia) prob_range = prob_range / sum(prob_range); % normalise the densities to exactly one S1 = zeros(length(t),1); % initialise the survival probability over time with zeros for i = 1:n % run through the different thresholds haz = bw * max(0,Dw-z_range(i)); % calculate hazard for each NEC cumhaz = cumtrapz(t,haz); % integrate the hazard rate numerically surv = min(1,exp(-1*cumhaz)); % calculate survival probability S1 = S1 + surv * prob_range(i); % add to S1, weighted for this NECs prob density end S = S .* S1; % make sure to add background hazard end Xout(:,glo.locS) = S; % replace correct state by newly calculated survival prob. [~,loct] = ismember(t_rem,t); % find where the requested time points are in the long Xout Xout = Xout(loct,:); % only keep the ones we asked for %% Events function % Modify this part of the code if _eventson_=1. % This subfunction catches the 'events': in this case, it looks for the % internal concentration where the threshold is exceeded (only when % useode=1). This only makes sense for SD. % % Note that the eventsfun has the same inputs, in the same sequence, as % <derivatives.html derivatives.m>. function [value,isterminal,direction] = eventsfun(t,X,par,c) global glo mw = par.mw(1); % threshold for effects nevents = 1; % number of events that we try to catch value = zeros(nevents,1); % initialise with zeros value(1) = X(glo.locD) - mw; % thing to follow is dose metric minus threshold isterminal = zeros(nevents,1); % do NOT stop the solver at an event direction = zeros(nevents,1); % catch ALL zero crossing when function is increasing or decreasing